- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Functions and Types of Functions
Functions
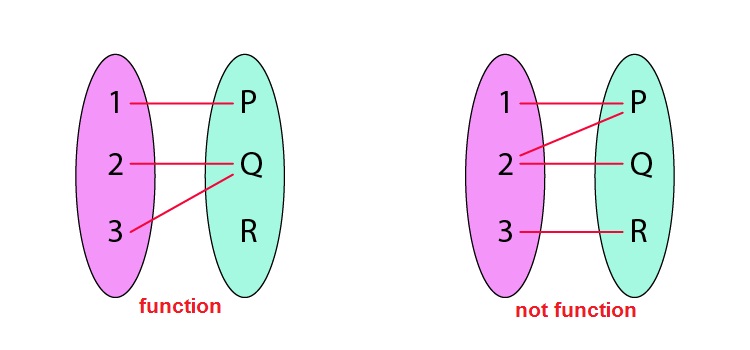
Function is a special type of relation.
Definition:-
A relation 'f' is said to be a function, if every element of a non-empty set X, has only one image or range to a non-empty set Y. Or. If 'f' is the function from X to Y and (x,y) ∊ f, then f(x) = y, where y is the image of x, under function f and x is the preimage of y, under 'f'.
Or
A relation ‘f’ is said to be a function, if every element of a non-empty set X, has only one image or range to a non-empty set Y.
Or
If ‘f’ is the function from X to Y and (x,y) ∊ f, then f(x) = y, where y is the image of x, under function f and x is the preimage of y, under ‘f’. It is denoted as;
f: X → Y.
Example: N be the set of Natural numbers and the relation R be defined as;
R = {(a,b) : b=a2, a,b ∈ N}. State whether R is a relation function or not.
Solution: From the relation R = {(a,b) : b=a2, a,b ∈ N}, we can see for every value of natural number, their is only one image. For example, if a=1 then b =1, if a=2 then b=4 and so on.
Therefore, R is a relation function here.
Types of Functions
There are various types of functions in mathematics which are explained below in detail. The different function types covered here are:
- One – one function (Injective function)
- Many – one function
- Onto – function (Surjective Function)
- Into – function
- Bijective – function
- Inverse -- function
One – one function (Injective function)
If each element in the domain of a function has a distinct image in the co-domain, the function is said to be one – one function.
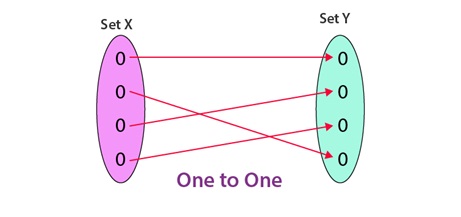
For examples f; R ->R given by f(x) = 3x + 5 is one – one.
Many – one function
On the other hand, if there are at least two elements in the domain whose images are same, the function is known as many to one.
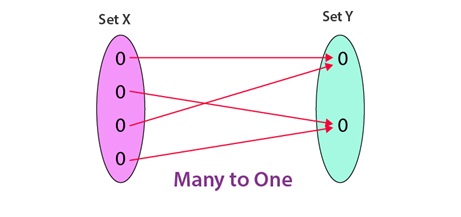
For example f : R-> R given by f(x) = x2 + 1 is many one.
Onto – function (Surjective Function)
A function is called an onto function if each element in the co-domain has at least one pre – image in the domain.
Into – function
If there exists at least one element in the co-domain which is not an image of any element in the domain then the function will be Into function.
(Q) Let A = {x : 1 < x < 1} = B be a mapping f : A ->B, find the nature of the given function (f).
f(x) = |x|
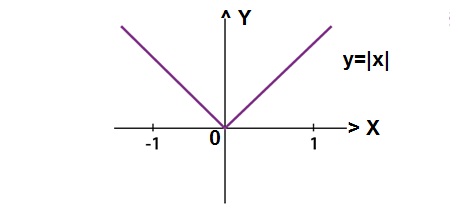
f (x) = |1|
Solution for x = 1 & -1
Hence it is many one the Range of f(x) from [-1, 1] is
[0,1] which is not equal to co-domain. Hence it is into function.
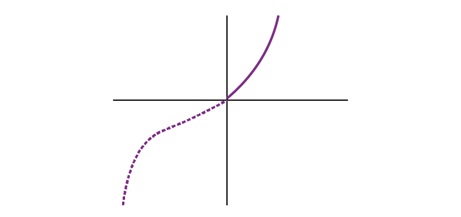
Lets say we have function,
f(x)={x2;x≥0−x2;x<0

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
