1. The slope of line and angles between two lines

Chapter 10

Straight Lines

The slope of line and angles between two lines:

A line is sometimes called a straight line or, more archaically, a right line (Casey 1893), to emphasize that it has no "wiggles" anywhere along its length. While lines are intrinsically one-dimensional objects, they may be embedded in higher dimensional spaces. Harary (1994) called an edge of a graph a "line."

A straight line is just a line with no curves. So, a line that extends to both sides till infinity and has no curves is called a straight line.

The two properties of straight lines in Euclidean geometry are that they have only one dimension, length, and they extend in two directions forever.

Note: If the area of the triangle ABC is zero, then three points A, B and C lie on

a line, i.e., they are collinear.

Slope of a Line:

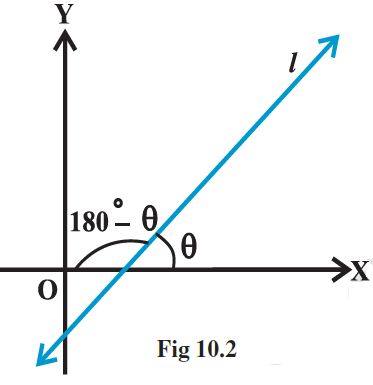
A line in a coordinate plane forms two angles with the x-axis, which are supplementary.

The angle (say) q made by the line l with positive direction of x-axis and measured anti clockwise is called the inclination of the line. Obviously 0° £ q £ 180°

lines parallel to x-axis, or coinciding with x-axis, have inclination of 0°. The inclination of a vertical line (parallel to or coinciding with y-axis) is 90°.

Definition: If q is the inclination of a line l, then tan q is called the slope or gradient of

the line l. The slope of a line whose inclination is 90° is not defined.

The slope of a line is denoted by m.

Thus, m = tan q, q ¹ 90°

It may be observed that the slope of x-axis is zero and slope of y-axis is not defined.

Slope of a line when coordinates of any two points on the line are given:

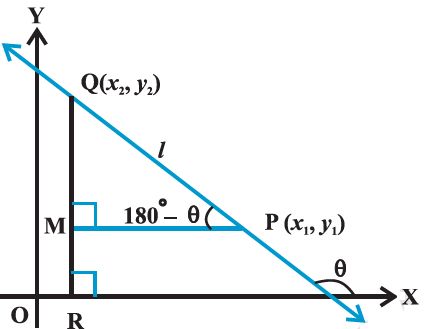
Let P(x1, y1) and Q(x2, y2) be two points on non-vertical line l whose inclination is q.

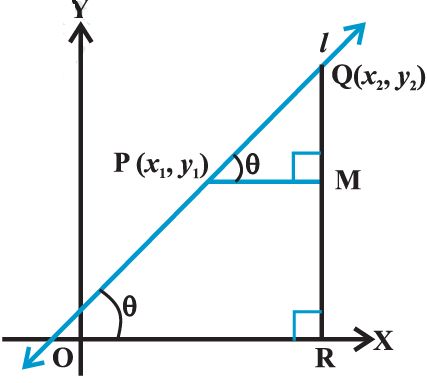
Case I When angle q is acute:

 ÐMPQ = q. ... (1)

Therefore, slope of line l = m = tan q.

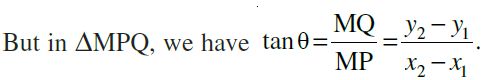
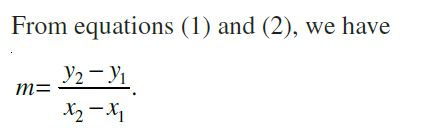
Case II When angle q is obtuse:

 we have ÐMPQ = 180° – q.

Therefore, q = 180° – ÐMPQ.

Now, slope of the line l

m = tan q

= tan ( 180° – ÐMPQ) = – tan ÐMPQ

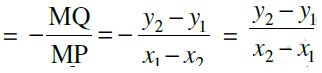
Example : Find the slope of the lines:

(a) Passing through the points (3, – 2) and (–1, 4),

(c) Passing through the points (3, – 2) and (3, 4),

(c) Making inclination of 30° with the positive direction of x-axis.

Solution: (a) The slope of the line through (3, – 2) and (– 1, 4) is

 m = (4 – (-2)) /(-1 – 3) = 6 / - 4 = -3/2

(b) The slope of the line through the points (3, – 2) and (3, 4) is

   m  = (4- (- 2)) / (3-3) = 6 / 0 , which is not defined.

(c) Here inclination of the line a = 60°. Therefore, slope of the line is

m = tan 30° = 1 / √3