5. Standard equations, Properties and Application of a hyperbola

Standard equations , Properties and Application of a hyperbola

Hyperbola

Definition : A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.

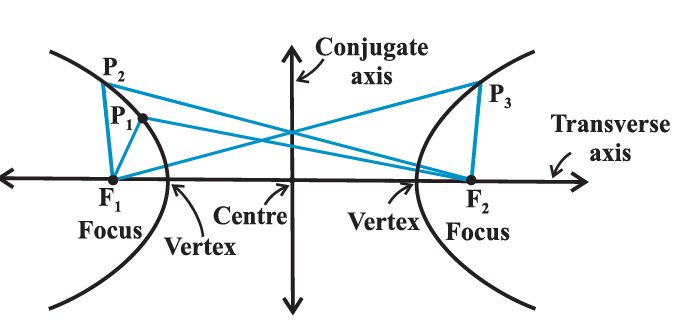
The term “difference” that is used in the definition means the distance to the farther point minus the distance to the closer point. The two fixed points are called the foci of the hyperbola. The mid-point of the line segment joining the foci is called the centre of the hyperbola. The line through the foci is called the transverse axis and the line through the centre and perpendicular to the transverse axis is called the conjugate axis. The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola.

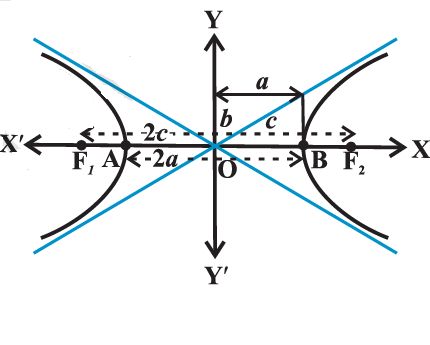
The distance between the two foci by 2c, the distance between two vertices (the length of the transverse axis) by 2a.

b= √(c²- a²)

2b is the length of the conjugate axis

we have

BF1 – BF2 = AF2 – AF1 (by the definition of the hyperbola)

BA +AF1– BF2 = AB + BF2– AF1

i.e., AF1 = BF2

So that, BF1 – BF2 = BA + AF1– BF2 = BA = 2a

Eccentricity

Definition : similarly, an ellipse, the ratio e = c / a is called the eccentricity of the

hyperbola. Since c ³a, the eccentricity is never less than one.

In terms of the eccentricity, the foci are at a distance of ae from the centre.

Standard equation of Hyperbola: The equation of a hyperbola is simplest if

the centre of the hyperbola is at the origin and the foci are on the x-axis or y-axis. The

two such possible orientations.

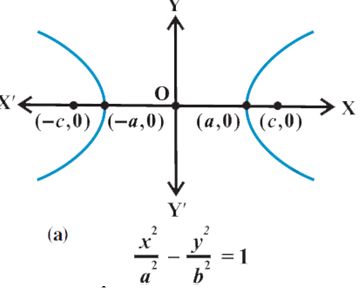
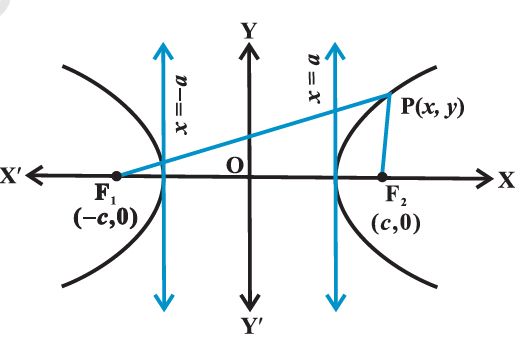
Let F1 and F2 be the foci and O be the mid-point of the line segment F1F2. Let O

be the origin and the line through O through F2 be the positive x-axis and

that through F1 as the negative x-axis.

Let P(x, y) be any point on the hyperbola such that the difference of the distances from P to the farther point minus the closer point be 2a.

So given, PF1 – PF2 = 2a

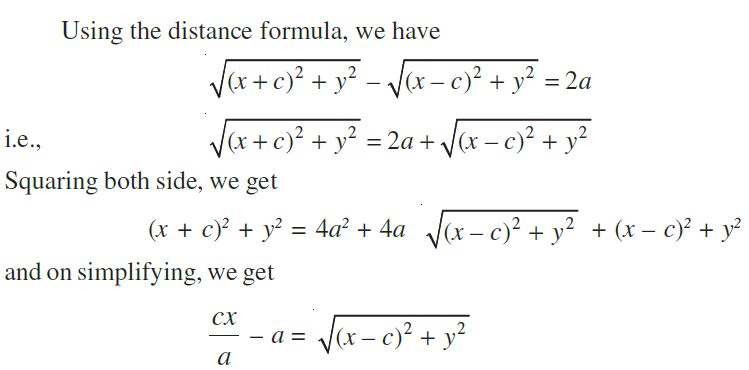
On squaring again and further simplifying, we get

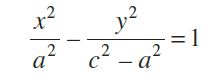 (Since c² – a² = b²)

Or

 

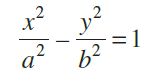
Note.: A hyperbola in which a = b is called an equilateral hyperbola.

Therefore, no portion of the curve lies between the

lines x = + a and x = – a, (i.e. no real intercept on the conjugate axis).

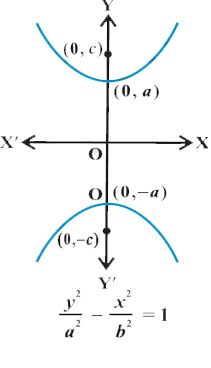
Similarly, we can derive the equation of the hyperbola.

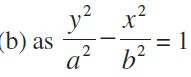
These two equations are known as the standard equations of hyperbolas.

 

Properties:

1. Hyperbola is symmetric with respect to both the axes, since if (x, y) is a point on the hyperbola, then (– x, y), (x, – y) and (– x, – y) are also points on the hyperbola.
2. The foci are always on the transverse axis. It is the positive term whose denominator gives the transverse axis.

 has transverse axis along x-axis of length 6.

 has transverse axis along y-axis of length 10.

Latus rectum:

Definition Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola.

The length of the latus rectum in hyperbola is 2b²/a

Example Find the equation of the hyperbola where foci are (0, ±12) and the length of the latus rectum is 36.

Solution Since foci are (0, ±12), it follows that c = 12.

Length of the latus rectum = 2b²/a = 36

or b² = 18a

Therefore c² = a² + b²; gives

144 = a² + 18a

i.e., a² + 18a – 144 = 0,

So a = – 24, 6.

Since a cannot be negative, we take a = 6 and so b² = 108.

Therefore, the equation of the required hyperbola is

Or,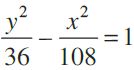

i.e., 3y² – x² = 108

Question :1 An ellipse passes through the foci of the hyperbola, 9x² −4y² =36 and its major and minor axes lie along the transverse and conjugate axes of the hyperbola respectively. If the product of eccentricities of the two conics is 1/2. Find the equation of ellipse.

Solution:

Equation of hyperbola is 9x² −4y² =36 or x²/4 − y²/9 = 1

(Here a < b)

Focus = (0, ± be)

Eccentricity = e = √(1+4/9) = √13/3

So, Foci of hyperbola: (0, ±√13)

Standard equation of the ellipse, x²/a² + y²/b² = 1 …(i)

Eccentricity = e’ = √(1-a²/b²) …(ii)

ee’ = 1/2 (given)

Using eccentricity value of hyperbola, e’ = 1/2 x 3/√13 = 3/2√13

(ii) e’² = (1-a²/b²)

9/52 = (1-a²/b²)

Find the value of b² form (i) using focii 13/b² = 1 => b² = 13

9/52 = (1-a²/13)

9/4 = 13 – a²

a² = 43/4

Now equation of ellipse is 4x²/43 + y²/13 = 1

 

Question 2: The locus of a point P(α, β) moving under the condition that the line y = αx + β is a tangent to the hyperbola x²/a² – y²/b² = 1 is

(a) an ellipse

(b) a circle

(c) a hyperbola

(d) a parabola

Answer: (c)

Solution:

Tangent to the hyperbola x²/a² – y²/b² = 1 is y = mx ± √(a²m² – b²)

Given that y = αx + β is the tangent of hyperbola.

m = α and a²m² – b² = β²

Therefore, a² α ² – b² = β²

Locus is a² x ² – y² = b² , which is parabola.