1. EQUILIBRIUM IN PHYSICAL PROCESSES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPTER – 7 EQUILIBRIUM
• Chemical Equilibrium
In a chemical reaction chemical equilibrium is defined as the state at which there is no further change in concentration of reactants and products.
For example,
Consider a hypothetical reaction,
A + B ↔ C + D
At equilibrium the rate of forward reaction is equal to the rate of backward reaction. Equilibrium
mixture: The mixture of reactants and products in the equilibrium state is called an equilibrium mixtures.
Based on the extent to which the reactions proceed to reach the state of equilibrium, these may be classified in three groups:
(i) The reactions which proceed almost to completion and the concentrations of the reactants left are negligible.
(ii) The reactions in which most of the reactants remains unchanged, i.e. only small amounts of products are formed.
(iii) The reactions in which the concentrations of both the reactants and products are comparable when the system is in equilibrium.
EQUILIBRIUM IN PHYSICAL PROCESSES
(i) Solid-Liquid Equilibrium: The equilibrium is represented as H2O(S) ↔ H2O(l)
Rate of melting of ice = Rate of freezing of water.
The system here is in dynamic equilibriums and following can be inferred.
(a) Both the opposing processes occur simultaneously
(b) Both the processes occur at the same rate so that the amount of ice and water – remains constant.
(ii) Liquid-Vapour Equilibrium
The equilibrium can be represented as
Rate of evaporation = Rate of condensation
When there is an equilibrium between liquid and vapours, it is called liquid-vapour equilibrium.
(iii) Solid-Vapour Equilibrium
This type of equilibrium is attained where solids sublime to vapour phase. For example, when solid iodine is placed in a closed vessel, violet vapours start appearing in the vessel whose intensity increases with time and ultimately, it becomes constant.
The equilibrium may be represented as I2 (s) ↔ I2 (vapour)
Rate of sublimation of solid I2 to from vapour = rate of condensation of I2 vapour to give solid I2.
• Equilibrium involving Dissolution of Solid in Liquid
Solution: When a limited amount of salt or sugar or any solute dissolves in a given amount of water solution is formed.
At a given temperature state is reached when no more solute can be dissolved then the solution is called saturated solution.
The equilibrium between a solid and its solution is indicated by the saturated solution and may be represented as
Rate of dissolution = rate of precipitation
Sugar (s) ↔ Sugaer (in solution)
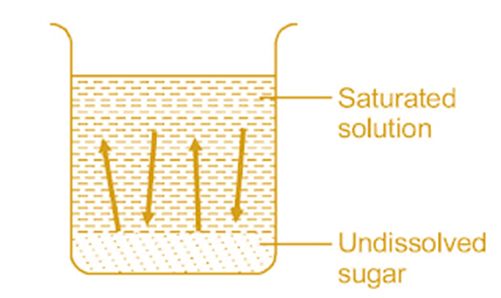
Here dissolution and precipitation takes place with the same speed.
On adding a small amount of radioactive sugar to the saturated solution it will be found that the sugar present in the solution as well as in the solid state is radioactive.
• Equilibrium between a Gas and its Solution in Liquid
This type of equilibrium can be seen by the following example:
Let us consider a sealed soda water bottle in which C02 gas is dissolved under high pressure. A state of equilibrium is attained between CO2 present in the solution and vapours of the gas
CO2(g) ↔ CO2 (present in solution)
Henry’s law: The solubility of a gas in a liquid at a certain temperature is governed by Henry’s law. It states that the mass of a gas that dissolves in a given mass of a solvent at any temperature is proportional to the pressure of the gas above the surface of the solvent.
Mathematically,
m ∝ p
m = KH p
where, KH = Henry’s constant
• Characteristics of Equilibria Involving Physical Processes
(i) The equilibrium can be attained only in closed systems at a given temperature.
(ii) At the equilibrium the measurable properties of the system remain constant.
(iii) The equilibrium is dynamic since both the forward and backward processes occur at same rate.
(iv) At equilibrium, the concentrations of substances become constant at constant temperature.
(v) The value of equilibrium constant represents the extent to which the process proceeds before equilibrium is achieved.
2. EQUILIBRIUM IN CHEMICAL PROCESSES – DYNAMIC EQUILIBRIUM
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
EQUILIBRIUM IN CHEMICAL PROCESSES
Like equilibria in physical systems it can also be achieved in chemical process involving reversible chemical reactions carried in closed container. A + B ↔ C + D
The dynamic nature of chemical equilibrium can be demonstrated in the synthesis of ammonia by Haber’s process. Haber started his experiment with the known amounts of N2 and H2 at high temperature and pressure. At regular intervals of time he determined the amount of ammonia present. He also found out concentration of unreacted N2 and H2.
After a certain time he found that the composition of mixture remains the same even though some of the reactants are still present. This constancy indicates the attainment of equilibrium. In general, for a o can be shown by
According to the equilibrium law,
![]()
Where Kc is called equilibrium constant.
For a general reaction,
aA + bB ↔ cC + dD
![]()
For the reactio H2 + I2 ↔ 2HI ;
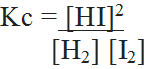
For the reaction N2 + 3H2 ↔ 2NH3
![]()
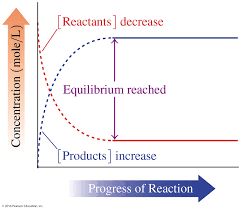
After a certain time the two reactions occur at the same rate and the system reaches a state of equilibrium. This can be shown by the given figure.
Equilibrium constant for the reverse reaction is the inverse of that for the forward reaction.
If the equilibrium constant for the reaction H2 + I2 ↔ 2HI is Kc, then that for the reverse reaction 2HI ↔ H2 + I2 is 1/Kc
3. LAW OF CHEMICAL EQUILIBRIUM AND EQUILIBRIUM CONSTANT
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
LAW OF CHEMICAL EQUILIBRIUM
At a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation. Let us consider the reaction,
![]()
Chemical equilibrium is defined as a state where both products along with reactants are present in the concentration and have no tendency to change further with time. There will be no observable changes in the properties of any particular system in the present. The equilibrium rates of forward and backward reactions are equal.
For example, the mixture of products and the reactants are in the equilibrium state.
In equilibrium, two opposite reactions act in equal rules or velocities, and therefore there are no changes in the substances involved. At this particular point, the reaction must be considered complete. The quantitative formulation is a reversible reaction A ⇋ B + C of equilibrium, the reaction’s velocity to its right, r1, which mathematical expression gives is based on the law of mass action. In “r1 = k1 (A)”, here the k1 is ratio rate.
A catalyst addition can affect both the backward & forward reaction in the same way and do not affect the equilibrium constant. Both the reactions will speed up with the help of a catalyst and increase the speed from which the equilibrium rate can be reached.
The law of chemical equilibrium helps to properly understand the rate of forward as well as backward reaction and rate of change in a chemical reaction.
The rate of forwarding reaction = rate of backward reaction.
The formula mentioned above is known as the Law of chemical equilibrium. Here K is considered an equilibrium constant, and it defines the molar concentration of the product. By the statement of the law of chemical equilibrium, we get to understand the ratio between the product’s concentration and the reactant’s concentration which are both raised to a power of stoichiometric coefficient that is said to be constant, provided that the temperature does not vary. This is called an equilibrium constant. This ratio defines the amount of reactant and product used to understand and analyze the chemical behaviour. This is the law of chemical equilibrium and equilibrium constant.
This constant can be presented as the partial pressures of the products along with reactants for gas-phase reactions. If this is expressed by partial pressure, then the K is represented as Kp.
Here, Pa, Pb, Pc, Pd are the partial pressures of a,b,c,d in the mixture of reactions.
●Examples of chemical equilibrium
To understand the law of chemical equilibrium better, let us analyze an experiment on hydrogen and iodine. The vapor of these two products is kept on a closed vessel at a constant temperature. The reaction starts to proceed and then stops after some time by converting some portion of iodine and hydrogen to hydrogen iodide. The reason for stopping the process was that the two constants reached the equilibrium level after reaching a particular point of dynamism.
Similarly, let us take some amount of hydrogen iodide in the closed vessel and keep it at the same constant temperature after some time. It will be converted into hydrogen molecules and iodine molecules. Therefore, the rest of the product will remain unchanged. However, two constants will remain the same and be fixed in both the experiment and reaction. This reaching of the dynamic stage is called the equilibrium.
Chemical equation: H2 (gas) + I2 (gas) ⇌ 2HI (gas)
4. HOMOGENEOUS EQUILIBRIA
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
HOMOGENEOUS EQUILIBRIUM
Homogeneous equilibrium is more straightforward and less complex when compared to Heterogeneous equilibrium. The most common examples are reactions that involve components in the gaseous state or solution reactions.
e.g.: Reaction of Nitrogen and Hydrogen to form Ammonia (Haber’s process)
N2(g)+ 3H2(g) ⇔ 2NH3(g)
The Esterification reaction between an alcohol and an organic acid is the best example of a liquid phase homogeneous reaction.
CH3COOH(l) + CH3CH2OH(l) ⇔ CH3COOCH2CH3(l) +H2O(l)
The equilibrium constant is a number that expresses the relationship between the concentration of products and the reactants in an equilibrium reaction at a given temperature. It is expressed as ‘Kc’. To derive the expression of Kc, let us consider the homogenous equilibrium equation,
aA + bB ⇔ cC + dD
Note that the products of the reaction are always written on the right side and the reactants are on the left side. The Equilibrium constant Kc for this reaction would consist of a ratio where the products with their coefficient as exponent forms the numerator and similarly the reactants form the denominator.
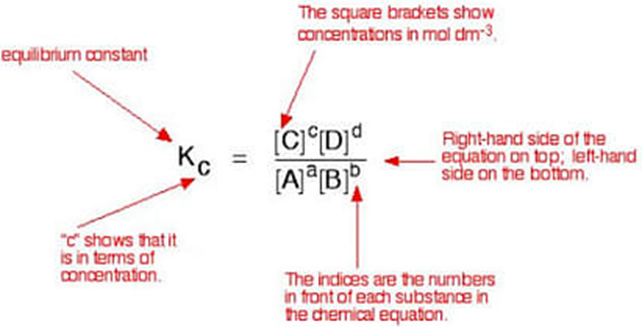
Example: Let us write the Equilibrium Constant expression Kc for the Haber’s process of Ammonia production
N2(g)+ 3H2(g) ⇔ 2NH3(g)
Kc is written as:
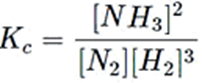
Note that for components that have only one molecule such as for N2, the exponential power of 1 need not be written. The concentration of only the gaseous and aqueous components in the reactions are taken into account.
Equilibrium Constant in Gaseous Systems
For an equilibrium reaction that involves gases, equilibrium constants should be expressed in terms of partial pressure. Thus the ideal gas equation is taken into account.
pV = nRT ……(Ideal gas equation)
→ p = n/V x RT
p → Pressure in Pa
n → Number of moles of gas
V → Volume in cu.m
T → Temperature in K
Here n/V expresses the concentration in moles/m³
Thus, p = c RT
Where c is the concentration in moles/lit
We can also write,
p = [gas] RT
Therefore, at a constant temperature, the pressure of a gas is directly proportional to its concentration.
Consider the reaction
aA + bB ⇔ cC + dD
Kc is written as,
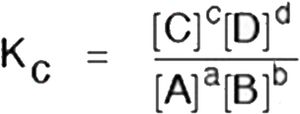
In terms of partial pressure, Kp is written as
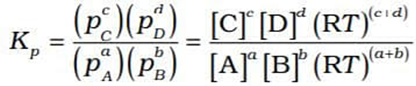 ( as p = [gas] RT)
( as p = [gas] RT)
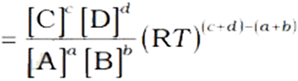
On substitution, we get the relation between Kc and Kp
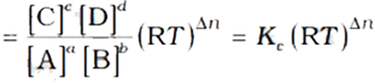
Where, Δn → (number of moles of gaseous products) - (number of moles of gaseous reactants)
5. HETEROGENEOUS EQUILIBRIA
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
HETEROGENEOUS EQUILIBRIA
The equilibrium reactions in which the reactants and the products are not present in the same phase are called heterogeneous equilibrium reactions. Such equilibria in which the reactants and products are not all in the same phase are called heterogeneous equilibria. Heterogeneous equilibrium is demonstrated by the breakdown of calcium carbonate into calcium oxide and carbon dioxide when heated. The following equilibrium is obtained if the reaction is carried out in a closed vessel.
CaCO3(s)⇌CaO(s) + CO2(g)CaCO3(s)⇌CaO(s) + CO2(g)
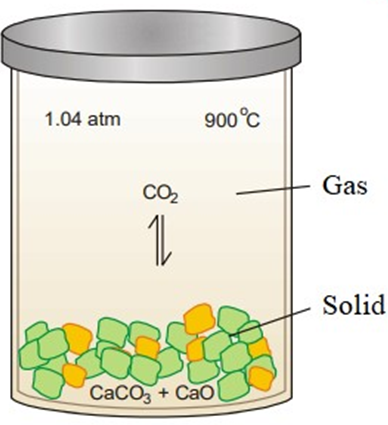
Some other examples of heterogeneous equilibria are:
NH4Cl(s)⇌NH3(g) + HCl(g)
3Fe(s) + 4H2O(g)⇌Fe3O4(s) + 4H2(g)
●Quantitative Characteristics of Heterogeneous Equilibria
An important point to note is that in the case of heterogeneous equilibria, the expression for equilibrium constant does not include the concentrations of pure solids and pure liquids as their concentrations remain constant. In other words, the concentration (moles per unit volume) of a pure solid (or liquid) is fixed and cannot vary. Thus, the concentrations of pure solids or liquids are not included in the equilibrium constant expression. For example, consider the following heterogeneous reaction,
CaCO3(s)⇌CaO(s) + CO2(g)
The equilibrium constant expression for this reaction is:
Kc = [CO2][CaO][CaCO3] CO2
But CaCO3 and CaO are pure solids. So, their concentrations may be assumed to be constant and can be ignored in the equilibrium constant expression. So the equilibrium constant expression for this reaction can be written as
Kc = [CO2]
Since the partial pressure of a gaseous component is proportional to its concentration,
Kp = pco2
As a result, we can deduce that when CaCO3 decomposes at a specific temperature, the equilibrium partial pressure of carbon dioxide gas equals its equilibrium constant in terms of partial pressure. In other words, there is constant pressure of carbon dioxide gas in equilibrium with calcium carbonate and calcium oxide at a particular temperature. So, it gives us a very easy method to find the value of Kp. For this, we need to measure the pressure of carbon dioxide gas in equilibrium with calcium carbonate and calcium oxide at a particular temperature.
Similarly, consider the following reaction:
2H2O(l)⇌2H2(g) + O2(g)
After ignoring the concentration for liquid water, its equilibrium constant expression becomes:
Kc = [H2]2[O2]
Kp = (pH2)2(pO2)
●Some Important Points Regarding Heterogeneous Equilibria
For heterogeneous chemical reactions, the concentration of pure solids and pure liquids are not included in the expression for the equilibrium constant. By convention
[solid]=1 and [liquid]=1
When the substance occurs in the liquid solutions, their concentrations are variable, and therefore their concentrations are given in the expression for the equilibrium constant.
It must be noted that pure substances must be present (however small it may be) for the equilibrium to exist, but they do not appear in the expression for the equilibrium constant.
The concentration of the solvent is considered constant because it is present in large quantities and will not change appreciably.
6. APPLICATIONS OF EQUILIBRIUM CONSTANTS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
APPLICATION OF EQUILIBRIUM CONSTANT
The knowledge of equilibrium constant helps us to
1. predict the direction in which the net reaction will take place
2. predict the extent of the reaction and
3. calculate the equilibrium concentrations of the reactants and products.
It is to be noted that these constants do not provide any information regarding the rates of the forward or reverse reactions.
1. Predicting the extent of a reaction
The value of equilibrium constant, Kc tells us the extent of a reaction, i.e., it indicates how far the reaction has proceeded towards product formation at a given temperature. A large value of Kc indicates that the reaction reaches equilibrium with high product yield. On the other hand, a low value of Kc indicates that the reaction reaches equilibrium with low product formed. In general, if the Kc is greater than the 103, the reaction proceeds nearly to completion. If it is less than 10-3, the reaction rarely proceeds. If the Kc is in the range 10-3 to103, significant amount of both reactants and products are present at equilibrium.
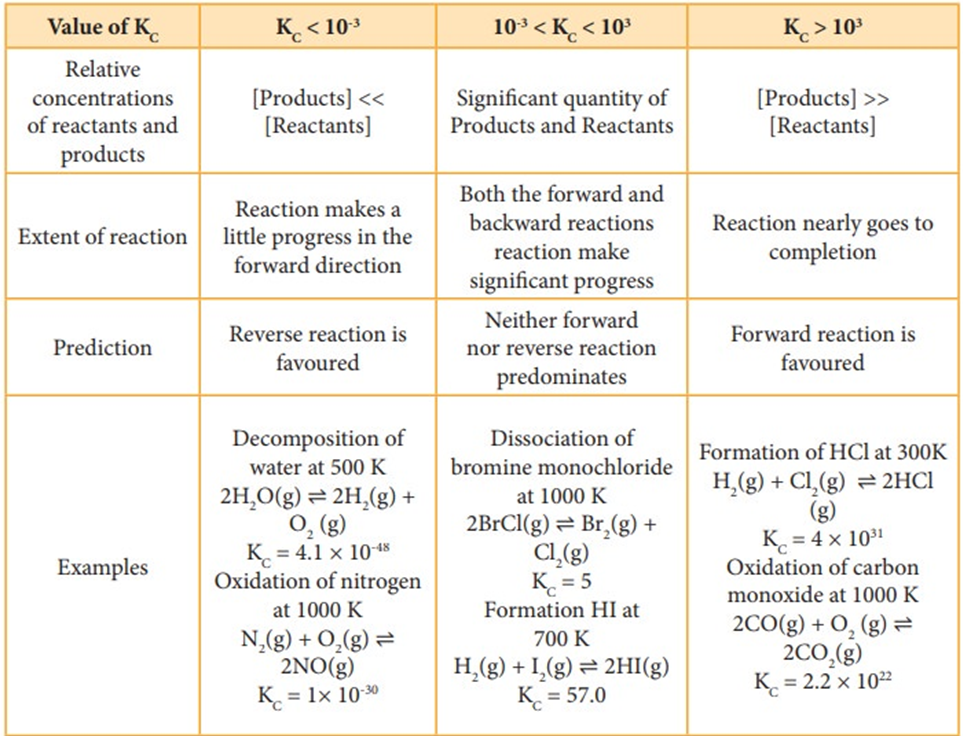
Example
Consider the following equilibrium reactions and relate their equilibrium, constants

2. Predicting the direction of a reaction
From the knowledge of equilibrium constant, it is possible to predict the direction in which the net reaction is taking place for a given concentration or partial pressure of reactants and products.
Consider a general homogeneous reversible reaction,
xA + yB ⇌ lC + mD
For the above reaction under non-equilibrium conditions, reaction quotient ‘Q’ is defined as the ratio of the product of active masses of reaction products raised to the respective stoichiometric coefficients in the balanced chemical equation to that of the reactants.
Under non-equilibrium conditions, the reaction quotient Q can be calculated using the following expression.
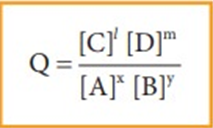
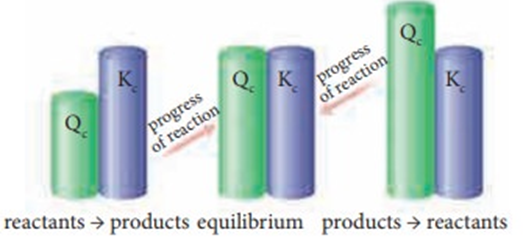
As the reaction proceeds, there is a continuous change in the concentration of reactants and products and also the Q value until the reaction reaches the equilibrium. At equilibrium Q is equal to Kc at a particular temperature. Once the equilibrium is attained, there is no change in the Q value. By knowing the Q value, we can predict the direction of the reaction by comparing it with Kc.
· If Q = Kc, the reaction is in equilibrium state.
· If Q > Kc, the reaction will proceed in the reverse direction i.e., formation of reactants.
· If Q < Kc, the reaction will proceed in the forward direction i.e., formation of products.
Example 1
The value of Kc for the following reaction at 717 K is 48.
H2(g) + I2(g) ⇌ 2HI(g)
At a particular instant, the concentration of H2, I2and HI are found to be 0.2 mol L-1, 0.2 mol L-1 and 0.6 mol L-1 respectively. From the above information we can predict the direction of reaction as follows.
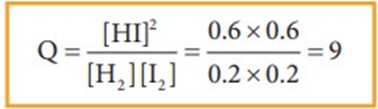
Since Q< Kc, the reaction will proceed in the forward direction.
Example 2
The value of Kc for the reaction
N2O4 (g) ⇌ 2NO2(g)
Kc = 0.21 at 373 K. The concentrations N2O4 and NO2 are found to be 0.125 mol dm-3 and 0.5 mol dm-3 respectively at a given time. From the above information we can predict the direction of reaction as follows
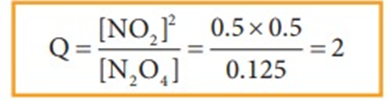
The Q value is greater than Kc. Hence, the reaction will proceed in the reverse direction until the Q value reaches 0.21
3. Calculation of concentration of reactants and products at equilibrium
If the equilibrium concentrations of reactants and products are known for a reaction, then the equilibrium constant can be calculated and vice versa.
Let us consider the formation of HI in which, ‘a’ moles of hydrogen and ‘b’ moles of iodine gas are allowed to react in a container of volume V. Let ‘x’ moles of each of H2 and I2 react together to form 2x moles of HI.
H2 (g)+ I2 (g) ⇌ 2HI2(g)

Applying law of mass action,

The equilibrium constant Kp can also be calculated as follows:
We know the relationship between the Kc and Kp

Solved Problem
One mole of H2 and one mole of I2 are allowed to attain equilibrium. If the equilibrium mixture contains 0.4 mole of HI. Calculate the equilibrium constant.
Given data:
[H2] = 1 mole [I2] = 1 mole
At equilibrium, [HI] = 0.4 mole Kc= ?
Solution:
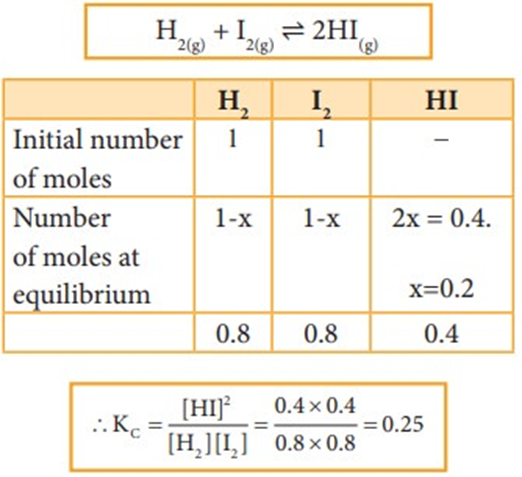
Dissociation of PCl5:
Consider that ‘a’ moles of PCl5 is taken in a container of volume V. Let ‘x’ moles of PCl5 be dissociated into x moles of PCl3 and x moles of Cl2.
PCl5(g) ⇌ PCl3(g) + Cl2(g)
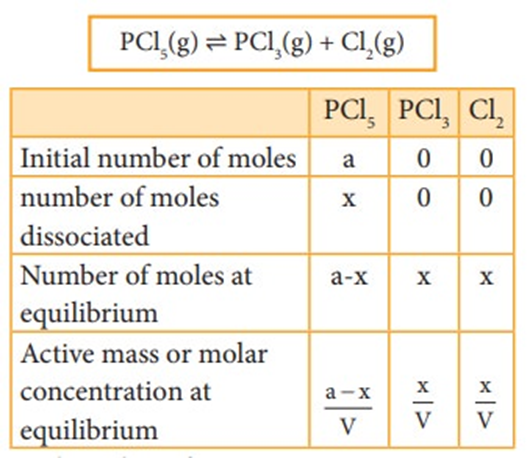
Applying law of mass action,
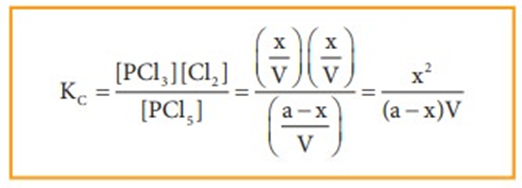
The equilibrium constant Kp can also be calculated as follows:
We know the relationship between the Kc and Kp

Where n is the total number of moles at equilibrium.
n = (a-x) + x + x = (a+x)
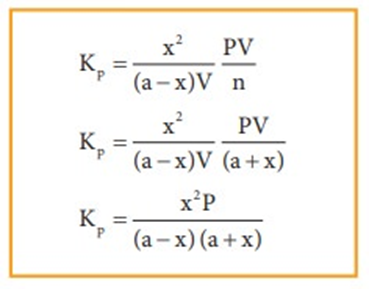
Synthesis of ammonia:
Let us consider the formation of ammonia in which, ‘a’ moles nitrogen and ‘b’ moles hydrogen gas are allowed to react in a container of volume V. Let ‘x’ moles of nitrogen react with 3x moles of hydrogen to give 2x moles of ammonia.
N2(g) + 3H2(g) ⇌ 2NH3(g)
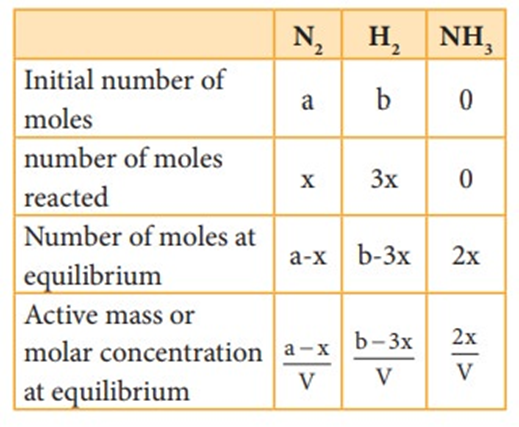
Applying law of mass action,
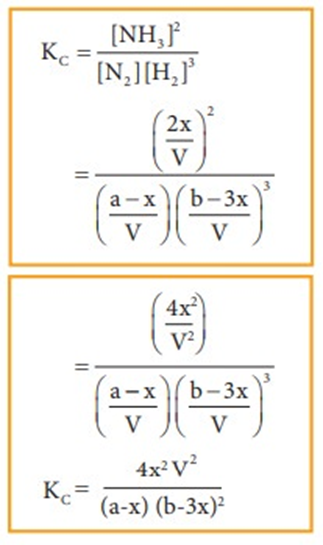
The equilibrium constant Kp can also be calculated as follows:

Total number of moles at equilibrium,
n= a-x + b-3x+ 2x = a+b-2x

Solved Problems:
The equilibrium concentrations of NH3, N2 and H2 are 1.8 × 10-2 M, 1.2 × 10-2 M and 3 × 10-2 M respectively. Calculate the equilibrium constant for the formation of NH3 from N2 and H2. [Hint: M= mol lit-1]
Given data:
[NH3] = 1.8 × 10-2 M
[N2] = 1.2 × 10-2 M
[H2] = 3 × 10-2 M
Kc = ?
Solution:
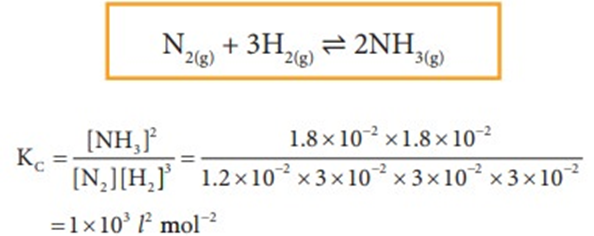
2. The equilibrium constant at 298 K for a reaction is 100.
A + B ⇌ C + D
If the initial concentration of all the four species is 1 M, the equilibrium concentration of D (in mol lit-1) will be
Given data:
[A] = [B] = [C]= [D] =1 M
Kc = 100
[D]eq = ?
Solution:
Let x be the no moles of reactants reacted

7. RELATIONSHIP BETWEEN EQUILIBRIUM CONSTANT K, REACTION QUOTIENT Q AND GIBBS ENERGY G
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
RELATIONSHIP BETWEEN EQUILIBRIUM CONSTANT K, REACTION QUOTIENT Q AND GIBBS ENERGY G.
A mathematical expression of thermodynamic view of equilibrium can be described by tine equation.
ΔG = ΔGº + RT InQ
Where, ΔGº is standard Gibbs energy.
At equilibrium, ΔG = 0 and Q = Kc, so the equation becomes,
0 = ΔGº + RT In Kc
Or, ΔGº = - RT InKc
On changing the base we get ΔGº = -2.303RT log Kc
We know that for a spontaneous process ΔG should be negative. So the value of Kc should be positive.
8. FACTORS AFFECTING EQUILIBRIA
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
FACTORS AFFECTING EQUILIBRIA
Le Chatelier’s principle: If a system under equilibrium is subjected to a change in temperature, pressure or concentration, then the equilibrium shifts in such a manner as to reduce or to counteract the effect of change.
Effect of Change of Concentration: When the concentration of any of the reactants or products in a reaction at equilibrium is changed, the composition of the equilibrium changes so as to minimise the effect.
Effect of Pressure Change
If the number of moles of gaseous reactants and products are equal, there is no effect of pressure.
When the total number of moles of gaseous reactants and total number of moles of gaseous products are different.
On increasing pressure, total number of moles per unit volume increases, thus the equilibrium will shift in direction in which number of moles per unit volume will be less.
If the total number of moles of products are more than the total number of moles of reactants, low pressure will favour forward reaction.
If total number of moles of reactants are more than total number of moles of products, high pressure is favourable to forward reaction.
Effect of Inert Gas Addition
If the volume is kept constant there is no effect on equilibrium after the addition of an inert gas.
Reason: This is because the addition of an inert gas at constant volume does not change the partial pressure or the molar concentration.
The reaction quotient changes only if the added gas is involved in the reaction.
Effect of Temperature Change
When the temperature of the system is changed (increased or decreased), the equilibrium shifts in opposite direction in order to neutralize the effect of change. In exothermic reaction low temperature favours forward reaction e.g.,

but practically very low temperature slows down the reaction and thus a catalyst is used. In case of endothermic reaction, the increase in temperature will shift the equilibrium in the direction of the endothermic reaction.
Effect of a Catalyst
Catalyst has no effect on the equilibrium composition of a reaction mixture.
Reason: Since catalyst increases the speed of both the forward and backward reactions to the same extent in a reversible reaction.
9. IONIC EQUILIBRIUM IN SOLUTION
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
IONIC EQUILIBRIUM IN SOLUTION
Electrolytes: Substances which conduct electricity in their aqueous solution.
Strong Electrolytes: Those electrolytes which on dissolution in water are ionized almost completely are called strong electrolytes.
Weak electrolyte: Those electrolytes which on dissolution in water partially dissociated are called weak electrolyte.
Ionic Equilibrium: The equilibrium formed between ions and unionised substance is called ionic equilibrium, e.g.,
10. ACIDS, BASES AND SALTS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ACIDS, BASES AND SALTS
Acids: Acids are the substances which turn blue litmus paper to red and liberate dihydrogen on reacting with some metals.
Bases: Bases are the substances which turn red litmus paper blue. It is bitter in taste. Common Example: NaOH, Na2C03.
• Arrhenius Concept of Acids and Bases
Acids: According to Arrhenius theory, acids are substances that dissociates in water to give hydrogen ions H+(aq).
Bases: Bases are substances that produce OH–(aq) after dissociation in water.
CH3COOH + H2O ↔ CH3COO- + H3O+
• Limitations of the Arrhenius Concept
(i) According to the Arrhenius concept, an acid gives H+ ions in water but the H+ ions does not exist independently because of its very small size (~H-18 m radius) and intense electric field.
(ii) It does not account for the basicity of substances like, ammonia which does not possess a hydroxyl group
• The Bronsted-Lowry Acids and Bases
According to Bronsted-Lowry, an acid is a substance which is capable of donating a hydrogen ion H+ and bases are substances capable of accepting a hydrogen ion H+.
In other words, acids are proton donors and bases are proton acceptors. This can be explained by the following example.
e.g. HCL is an acid since it produces H3O+ in aqueous solution.
HCl(l) + H2O(l) ↔ H3O+(aq) + Cl-(aq)
e.g. for base is NaOH
NaOH(s) + H2O(l) ↔ Na+(aq) + OH-(aq)
Note : H+ ions exist in water as hydronium ions (H3O+)
H+ + H2O ↔ H3O+
• Acid and Base as Conjugate Pairs
The acid-base pair that differs only by one proton is called a conjugate acid-base pair.
Let us consider the example of ionization of HCl in water.
For example in the reaction : NH3(l) + H2O(l) ↔ NH4+(aq) + OH-(aq)
Here water acts as a base because it accepts the proton.
CL is a conjugate base of HCl and HCl is the conjugate acid of base CL. Similarly, H20 is conjugate base of an acid H30+ and H30+ is a conjugate acid of base H2O.
• Lewis Acids and Bases
According to Lewis, acid is a substance which accepts electron pair and base is a substance with donates an electron pair.
Electron deficient species like AlCl3, BH3, H+ etc. can act as Lewis acids while species like H20, NH3 etc. can donate a pair of electrons, can act as Lewis bases.
11. IONIZATION OF ACIDS AND BASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
IONIZATION OF ACIDS AND BASES
Strength of acid or base is determined with the help of extent of ionization in aqueous solution.
pH Scale: Hydrogen-ion concentration are measured as the number of gram ions of hydrogen ions present per litre of solution. Since these concentrations are usually small, the concentration is generally expressed as the pH of the solution. pH being the logarithm of the reciprocal of the hydrogen ion concentration.
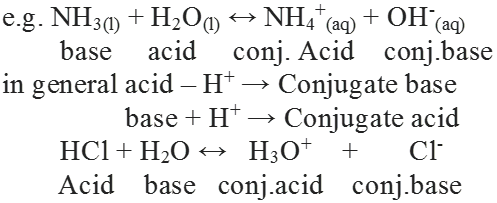
• Di and Polybasic Acids
Acids which contain more than one ionizable proton per molecule are called Dibasic acids or polybasic acids or polyprotic acids.
Common examples are oxalic acid, sulphuric acid, phosphoric acid etc.
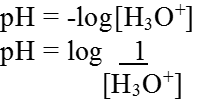
The pH range at 25º C is taken as 0 to 14.
pH = 7 Neutral
pH > 7 Basic
pH < 7 Acidic
The ionization reaction for a dibasic acid can be represented as:
H2X (aq) ↔ H+(aq) + HX-(aq)
HX-(aq) ↔ H+(aq) + X2-(aq)
Their equilibrium constant can be written as
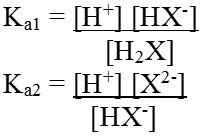
Ka1 and Ka2 are called first and second ionization constants respectively
For dibasic acid Ka1 > Ka2
Factors Affecting Acid Strength
When the strength of H-A bond decreases

The energy required to break the bond decreases, H-A becomes a stronger acid.
As the size of A increases down the group, H-A bond strength decreases and so the acid strength increases.
In a period, as the electronegativity of A increases, the strength of the acid increases.

• Common Ion Effect
If in a aqueous solution of a weak electrolyte, a strong electrolyte is added having an ion common with the weak electrolyte, then the dissociation of the weak electrolyte is decreased or suppressed. The effect by which the dissociation of weak electrolyte is suppresed is known as common ion effect.
CH3COOH(aq) ↔ CH3COO-(aq) + H+(aq)
• Hydrolysis of Salts and the pH of their Solutions
As per the hydrolysis formula,
For the salt of weak acid and weak base like CH3COONa
CH3COO- + Na+ H2O ↔ CH3COOH + Na+ + OH-
CH3COO- + H2O ↔ CH3COOH + OH-
Or,
After hydrolysis solution will be basic pH > 7
In this type of hydrolysis only anions of salt take part in the hydrolysis it is known as anionic hydrolysis.
Hydrolysis of weak acid and weak base
Salts belong to this type are CH3COONH4, (NH4)2CO3 etc.
CH3COONH4 + H2O ↔ CH3COOH + NH4OH
Or, CH3COO- + NH4+ + H2O ↔ CH3COOH + NH4OH
pH of the solution depends upon the relative strengths of acid and base.
12. BUFFER SOLUTIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
BUFFER SOLUTIONS
The solutions which resist charge in pH on dilution or with addition of small amounts of acid or alkali are called buffer solutions.
e.g. CH3COOH + CH3COONa
H2CO3 + HCl
Acidic Buffer: Weak acid and its salt with strong base are known as acidic buffer pH < 7.
e.g CH3COOH and CH3COONa, H2CO3 and HCl
Basic Buffer: Weak base and its salt with strong acid are known as basic buffer. pH > 7
e.g. NH4Cl and NH4OH
- pOH of a basic buffer = pKb + log ([salt]/[acid])
- pH of a basic buffer = pKa – log ([salt]/[acid])

13. SOLUBILITY EQUILIBRIA OF SPARINGLY SOLUBLE SALTS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
SOLUBILITY EQUILIBRIA OF SPARINGLY SOLUBLE SALTS
The solubility of a particular salt in a solvent is always a very significant fact to be taken into consideration when studying its properties and the properties of the solution it forms with a particular solvent. While salts like NaCl,KCl and others such as potassium dichromate are completely soluble in water, there are some salts that do not dissolve at all or dissolve only to a very minimal extent. These salts form a special case when defining the solubility equilibria and are called sparingly soluble salts.
Such sparingly soluble salts present solubility equilibria which are measured using an entity called a solubility product. This article will discuss the solubility product and how it can be applied to the solubility equilibria of sparingly soluble salts.
Salts are classified on the basis of their solubility in the following table.

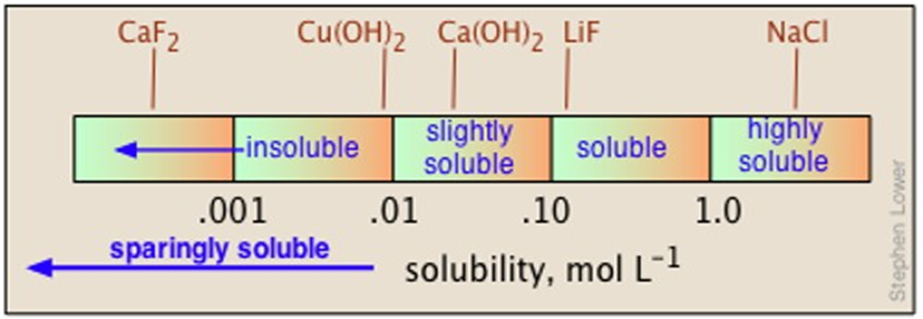
• Solubility Products
A sparingly soluble salt is so-called because when it is stirred into water or mixed with water, only a very small amount of the salt goes into the solution, and most of it remains undissolved. The solution becomes saturated with that little amount of salt dissolved, and the salt immediately dissociates into its ions. For example, when a sparingly soluble salt like AgCl goes into the solution, it dissociates as Ag+ and Cl− ions immediately. So, a dynamic equilibrium exists between the two entities: the undissolved salt and the dissolved ions which are in the solution.
At equilibrium, the dissolving of solid AgCl and precipitation of undissolved AgCl will take place at the same rate. Hence, the equilibrium between the two opposite processes can be given by a reversible equation:
AgCl(s) Dissolution/Precipitation ⇔ AgCl(aq) ↔ Ag+(aq) + Cl-(aq)
The equation can also be written as: AgCl(aq) ↔ Ag+(aq) + Cl–(aq)
When the law of chemical equilibrium is applied to the above equation, it can be written as: K = [Ag+][Cl–][AgCl]
The concentration of the undissolved solid AgCl usually remains constant, and hence, the above equation can be written as: [Ag+][Cl−]= K∗[AgCl] = Ksp
The Ksp is the solubility product and is equal to the ionic product: [Ag+][Cl−] in the saturated solution.
So, for any sparingly soluble salt solution, AxBy the equilibrium of the reaction can be represented as: AxBy ↔ xAy+ + yBx–
The solubility product for AxBy can be written as: Ksp = [Ay+]x ∗ [Bx–]y
The x and y represent the number of ions present in the formula of the sparingly soluble salt.
Hence, the solubility product at a specified temperature for an electrolyte can be defined as the product of the molar concentrations of the ions present in its saturated solution, with each concentration raised to the power equal to the number of ions produced on the dissociation of one molecule of the electrolyte.
Difference between Solubility Product and Ionic Product
As we know, the solubility product and the ionic product of an electrolyte is represented by the product of their concentrations, raised to a power that is equal to the number of ions present on its dissociation. So, how do we differentiate between the two of them? Here is how:
a. Ionic product is used for all types of solutions, both saturated and unsaturated. However, the solubility product is only used for saturated solutions, where a dynamic equilibrium exists between the undissolved salt and the dissolved ions present in the solution. So, one can call the solubility product the ionic product in saturated solutions.
b. For any salt, its solubility product is constant at a constant temperature. The ionic product, however, will depend upon the number of ions present at that particular time.
Solubility products of any sparingly soluble salt can be determined using the value of its solubility product in water at that temperature.
Significance of Solubility Product
The solubility product value can be applied in various aspects and, therefore, is very useful. Below are some of the applications of the solubility product of salts.
a. To Calculate the Solubility of Sparingly Soluble Salt: The solubility of a sparingly soluble salt is very difficult to measure. However, the knowledge of its solubility product can help in determining its solubility at any temperature.
The relationship between solubility (inmol/L) and solubility product (Ksp) depends upon the nature of the salt.
(i) Salts of type AB: (Example: PbSO4,AgCl,AgBr etc.)
AB ↔ A+ + B–
Ksp = [A+][B–] = s ∗ s = s2
(ii) Salts of type AB2:(PbCl2,SrF2)
AB2 ↔ A+ + 2B–
Ksp = [A+][B−] = s ∗ (2s)2 = s∗4 s2 = 4 s3
Similarly, it can be calculated for all other salts with different types to determine the relationship between solubility and solubility product.
b. To Predict Precipitation Reactions: We know that the solubility product of salt is its maximum saturation point at a particular temperature. So, it represents the upper limit in the ionic product of a sparingly soluble salt.
What that means is that if the ionic product is equal to Ksp then no more solute can go into that solution at that particular temperature. This can help in predicting the precipitation.
When the ionic product or the product of the concentration of ions in any solution is more than that of the value of its solubility product of that sparingly soluble salt, then the excess ions will result as a precipitate or precipitation will occur.
So, when two solutions containing known concentrations of ions are mixed together, the knowledge of their solubility product can help predict whether the precipitation will occur or not.
c. In Qualitative Analysis: The separation and identification of basic radicals are made based upon the principles of common ion effect and solubility product principle in qualitative analysis.
d. Precipitation of Soluble Salts: The use of solubility product and common ion effect explains the phenomenon of precipitation when a saturated solution is mixed with a suitable electrolyte containing a common ion. The increase in the ionic product over the solubility product results in precipitation. This phenomenon is used in the purification of common salt, salting out of soap and also in the manufacture of baking soda or sodium bicarbonate.
It is applicable to sparingly soluble salt. There is equilibrium between ions and unionised solid substance.
AgCl ↔ Ag+ + Cl-
Ksp = [Ag+] [Cl-]
Ksp is called solubility product
In pure water,
Ksp = [Ag+] [Cl-]
Ksp = S2 { ∵ S = [Ag+] = [Cl-] }
S = √Ksp
• Equilibrium: It can be established for both physical and chemical processes. At the state of equilibrium rate of forward and backward reactions are equal.
• Equilibrium constant: Kc is expressed as the concentration of products divided by reactants each term raised to the stoichiometric coefficients. For reactions,
aA + bB ↔ cC + dD
Kc = [C]ceq [D]deq
[A]aeq [B]beq
Kc >> 1 : Mixture contains mostly product
Kc << 1 : Mixture contains mostly reactants
• Le Chatelier’s principle: It states that the change in any factor such as temperature, pressure, concentration etc., will cause the equilibrium to shift in such a direction so as to reduce the effect of the change.
• Electrolytes: Substances that conduct electricity in aqueous solutions are called electrolytes.
• Arrhenius Concept: According to Arrhenius, acids give hydrogeneous while bases produce hydroxyl ions in their aqueous solution.
• Bronsted-Lowry concept: Bronsted-Lowry defined acid as proton donor and a base as a proton acceptor.
• Conjugate base and Conjugate acid: When a Bronsted-Lowry acid reacts with a base it produces its conjugate base and conjugate acid.
• Conjugate pair of acid and base: Conjugate pair of acid and base differs only by one proton.
• Lewis acids: Define acid as an electron pair acceptor and a base as an electron pair donor.
• pH Scale: Hydronium ion concentration in molarity is more conveniently expressed on a logarithmic scale known as the pH scale. The pH of pure water is 7.
• Buffer solution: It is the solution whose pH does not change by addition of small amount of strong acid or base.
For example: CH3COOH + CH3COONa.
• Solubility product (Ksp): For a sparingly soluble salt, it is defined as the product of molar concentration of the ions raised to the power equal to the number of times each ion occurs in the equation for solubilities.
BaSO4 ↔ Ba2+(aq) + SO42-(aq)
This equilibrium system may be described by the mass action expression

 Ritan Sheth
Ritan Sheth
