1. INTERMOLECULAR FORCES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPTER – 5 STATES OF MATTER
INTERMOLECULAR FORCES
Intermolecular forces are the forces of attraction and repulsion between interacting particles
have permanent dipole moments. This interaction is stronger than the London forces but is weaker than ion-ion interaction because only partial charges are involved.
The attractive forces decrease with the increase of distance between dipoles. The interaction energy is proportional to 1/r6 where r is the distance between polar molecules.
Ion-Dipole Interaction: This is the force of attraction which exists between the ions (cations or anions) and polar molecules. The ion is attracted towards the oppositely charged end of dipolar molecules.
The strength of attraction depends upon the charge and size of the ion and the dipole moment and the size of the polar molecule.
For example: Solubility of common salt (NaCl) in water.
• Ion-induced Dipolar Interactions
In this type of interaction permanent dipole of the polar molecule induces dipole on the electrically neutral molecule by deforming its electronic cloud. Interaction energy is proportional to 1/r6 where r is the distance between two molecules
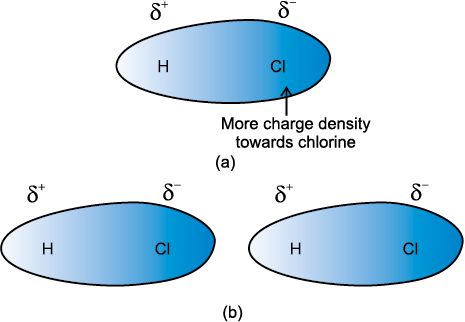
• London Forces or Dispersion Forces
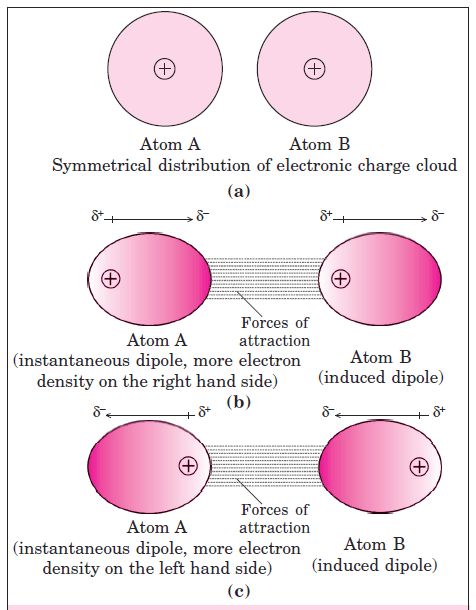
As we know that in non-polar molecules, there is no dipole moment because their electronic . charge cloud is symmetrically distributed. But, it is believed that at any instant of time, the electron cloud of the molecule may be distorted so that an instantaneous dipole or momentary dipole is produced in which one part of the molecule is slightly more negative than the other part. This momentary dipole induces dipoles in the neighbouring molecules. Thus, the force of attraction exists between them and are exactly same as between permanent dipoles. This force of attraction is known as London forces or Dispersion forces. These forces are always attractive and the interaction energy is inversely proportional to the sixth power of the
distance between two interacting particles, (i.e. 1/r6 where r is the distance between two particles). This can be shown by fig. given below.
Hydrogen bonding: When hydrogen atom is attached to highly electronegative element by covalent bond, electrons are shifted towards the more electronegative atom. Thus a partial positive charge develops on the hydrogen atom. Now, the positively charged hydrogen atom of one molecule may attract the negatively charged atom of some other molecule and the two molecules can be linked together through a weak force of attraction.
![]()
2. THERMAL ENERGY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
THERMAL ENERGY
The energy arising due to molecular motion of the body is known as thermal energy. Since motion of the molecules is directly related to kinetic energy and kinetic energy is directly proportional to the temperature.
3. INTERMOLECULAR FORCES vs THERMAL INTERACTIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
INTERMOLECULAR FORCES vs THERMAL INTERACTIONS
Intermolecular forces tend to keep the molecules together but thermal energy of the molecules tends to keep them apart. Three states of matter are the result of balance between intermolecular forces and the thermal energy of the molecules. When molecular interactions are very weak, molecules do not cling together to make liquid or solid unless thermal energy is reduced by lowering the temperature. Gases do not liquify on compression only, although molecules come very close to each other and intermolecular forces operate to the maximum. However, when thermal energy of molecules is reduced by lowering the temperature; the gases can be very easily liquified. Predominance of thermal energy and the molecular interaction energy of a substance in three states is depicted as follows
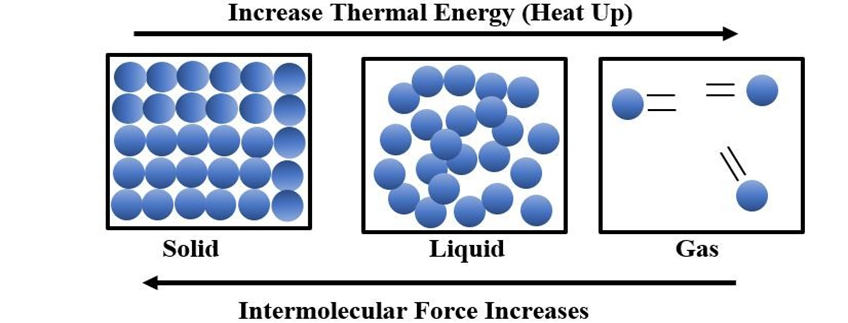
4. THE GASEOUS STATE
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
THE GASEOUS STATE
Physical Properties of Gaseous State
(i) ases have no definite volume and they do not have specific shape,
(ii) Gases mix evenly and completely in all proportions without any mechanical aid.
(iii) Their density is much lower than solids and liquids. :
(iv) They are highly compressible and exert pressure equally in all directions
5. THE GAS LAWS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
THE GAS LAWS
• Boyle’s Law (Pressure-Volume Relationship)
At constant temperature, the volume of a given mass of gas is inversely proportional to its pressure. It states that, under isothermal conditions pressure of a given mass of a gas is inversely proportional to its volume.
According to this the volume of a given mass of gas is inversely proportional to pressure at constant temperature. This law is given by Robert Boyle.
P ∝ 1 …… (at constant T and n)
V
P = k 1
V
Where k is the proportionality constant.
If a fixed amount of gas at constant temperature T occupying volume V1 at pressure P1 undergoes expansion so that volume becomes V2 and pressure becomes P2, then according to Boyle’s law.
P1V1 = P2V2 = constant
∴ P1 = V2
P2 V1
• Charles’ law:
At constant pressure, the volume of a given mass of a gas is directly proportional to its absolute temperature.
V ∝ T
or, V = constant
T
Let V1 be the volume of a gas at temperature T1. Pressure remains constant.
If the temperature of the gas increased to T2, then the volume will also increase to V2.
Therefore, according to law,
V1 = V2
T1 T2
• Gay Lussac’s Law (Pressure-Temperature Relationship)
At constant volume, pressure of a given mass of a gas is directly proportional to the temperature.
Mathematically,
P ∝ T
∴ P = k (at constant volume, and mass)
T
Where, k is the proportionality constant.
If a fixed amount of gas at constant volume V occupying pressure P1 at temperature T1 undergoes expansion, so that pressure becomes P2 and temperature becomes T2 then according to lussac’s law
P = constant
T
P1 = P2
T1 T2
• Avogadro Law (Volume-Amount Relationship)
Avogadro’s law states that equal volumes of all gases under the same conditions of temperature and pressure contain equal number of molecules. V α n
Where n is the number of moles of the gas.
Avogadro constant: The number of molecules in one mole of a gas
= 6.022 x 1023
Ideal Gas: A gas that follows Boyle’s law, Charles’ law and Avogadro law strictly, is called an ideal gas.
Real gases follow these laws only under certain specific conditions. When forces of interaction are practically negligible.
6. IDEAL GAS EQUATION
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
IDEAL GAS EQUATION
This is the combined gas equation of three laws and is known as ideal gas equation.
At constant T and n : V ∝ 1
P Boyle’s law
At constant P and n : V ∝ T Charle’s law
At constant P and T : V ∝ n Avogadro law
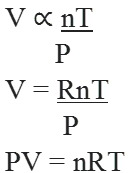
Where R is proportionality constant known as universal gas constant.
Numerical value or R
R = 0.0821 litre atm K-1 mol-1
R = 0.0831 litre bar K-1 mol-1
R = 8.314 J K-1mol-1
R = 1.987 ≈ 2 cal K-1 mol-1
R = 8.314 x 107 erg K-1 mol-1
If tempurature, volume and pressure of a fixed amount of gas vary from T1 , V1 and P1 to T2 , V2 and P2 then we can write,
![]()
This equation is also known as combined gas law.
• Dalton’s Law of Partial Pressure
When two or more non-reactive gases are enclosed in a vessel, the total pressure exerted by the gaseous mixture is equal to the sum of the partial pressure of individual gases.
Let P1 ,P2, and P3 be the pressure of three non reactive gases A, B, and C. When enclosed separately in the same volume and under same condition.
PTotal = P1+ P2 + P3
Where, PTotal = P is the total pressure exerted by the mixture of gases.
• Aqueous Tension
Pressure of non reacting gases are generally collected over water and therefore are moist. Pressure of dry gas can be calculated by substracting vapour pressure of water from total pressure of moist gas.
P2Dry gas = PTotal – Aqueous Tension
• Partial Pressure in terms of Mole Fraction
Let at the temperature T, three gases enclosed in the volume V, exert partial pressure P1 , P2 and P3 respectively, then
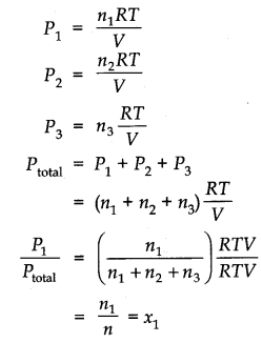
Where, (n = n1 + n2 + n3)
∴ P1 = n1 Ptotal
7. KINETIC ENERGY AND MOLECULAR SPEEDS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
KINETIC ENERGY AND MOLECULAR SPEEDS
Molecules of gases remain in continuous motion. While moving they collide with each other and with the walls of the container. This results in change of their speed and redistribution of energy.
So the speed and energy of all the molecules of the gas at any instant are not the same. Thus, we can obtain only average value of speed of molecules.
If there are n number of molecules in a sample and their individual speeds are u1, u2,…….un, then average speed of molecules uav can be calculated as follows:
uav = (u 1 + u 2 + .........u n) / n
Maxwell and Boltzmann have shown that actual distribution of molecular speeds depends on temperature and molecular mass of a gas. Maxwell derived a formula for calculating the number of molecules possessing a particular speed.
Fig. shows schematic plot of number of molecules vs. molecular speed at two different temperatures T1 and T 2 (T 2 is higher than T 1 ) . The distribution of speeds shown in the plot is called Maxwell-Boltzmann distribution of speeds.
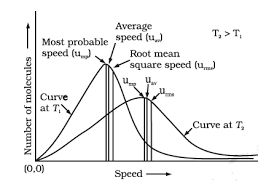
The graph shows that number of molecules possessing very high and very low speed is very small. The maximum in the curve represents speed possessed by maximum number of molecules .
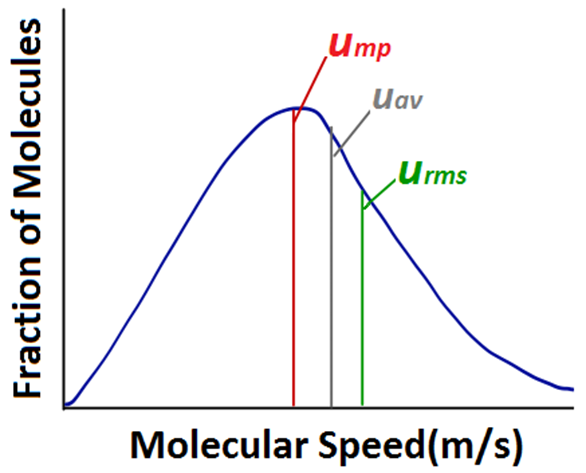
This speed is called most probable speed, ump. This is very close to the average speed of the molecules . On increasing the temperature most probable speed increases. Also, speed distribution curve broadens at higher temperature.
Broadening of the curve shows that number of molecules moving at higher speed increases. Speed distribution also depends upon mass of molecules. At the same temperature, gas molecules with heavier mass have slower speed than lighter gas molecules .
For example, at the same temperature lighter nitrogen molecules move faster than heavier chlorine molecules. Hence, at any given temperature, nitrogen molecules have higher value of most probable speed than the chlorine molecules. We know that kinetic energy of a particle is given by the expression:
Kinetic Energy = (1/2)mu2
Therefore, if we want to know average translational kinetic energy, for the movement of a gas particle in a straight line, we require the value of mean of square of speeds, of all molecules.
The mean square speed is the direct measure of the average kinetic energy of gas molecules. If we take the square root of the mean of the square of speeds then we get a value of speed which is different from most probable speed and average speed. This speed is called root mean square speed and is given by the expression as follows:
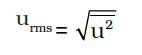
8. KINETIC MOLECULAR THEORY OF GASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
KINETIC MOLECULAR THEORY OF GASES
(i) Gases consist of large number of very small identical particles (atoms or molecules),
(ii) Actual volume occupied by the gas molecule is negligible in comparison to empty space between them.
(iii) Gases can occupy all the space available to them. This means they do not have any force of attraction between their particles.
(iv) Particles of a gas are always in constant random motion.
(v) When the particles of a gas are in random motion, pressure is exerted by the gas due to collision of the particles with the walls of the container.
(vi) Collision of the gas molecules are perfectly elastic. This means there is no loss of energy after collision. There may be only exchange of energy between colliding molecules.
(vii) At a particular temperature distribution of speed between gaseous particles remains constant.
(viii) Average kinetic energy of the gaseous molecule is directly proportional to the absolute temperature.
9. BEHAVIOUR OF REAL GASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
DEVIATION FROM IDEAL GAS BEHAVIOUR
Real Gas: A gas which does not follow ideal gas behaviour under all conditions of temperature and pressure, is called real gas. Deviation with respect to pressure can be studied by plotting pressure Vs volume curve at a given temperature. (Boyle’s law)
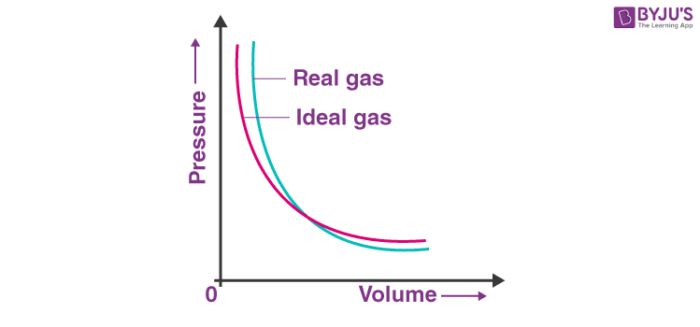
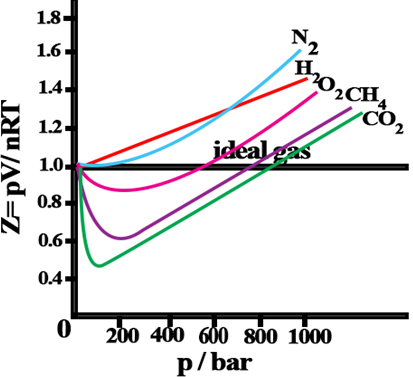
Compressibility factor (Z): Deviation from ideal behaviour can be measured in terms of compressibility factor, Z.
![]()
• van der Waals Equation
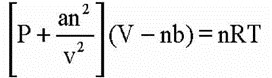
Where V is a constant for molecular attraction while ‘V is a constant for molecular volume.
(a) There is no force of attraction between the molecules of a gas.
(b) Volume occupied by the gas molecule is negligible in comparison to the total volume of the gas.
Above two assumptions of the kinetic theory of gas was found to be wrong at very high pressure and low temperature.
10. LIQUEFACTION OF GASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
LIQUIFACTION OF GASES
Liquifaction of gases can be achieved either by lowering the temperature or increasing the pressure of the gas simultaneously.
Thomas Andrews plotted isotherms of C02 at various temperatures shown in figure.
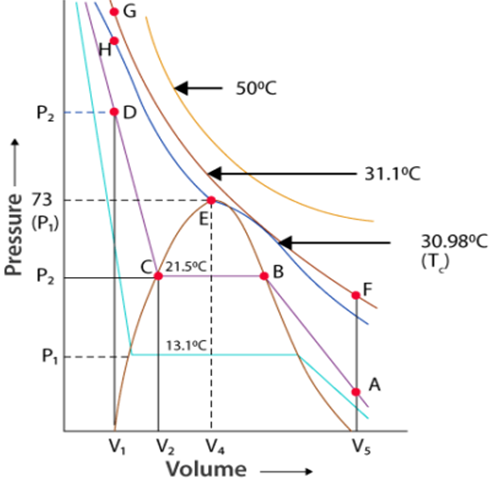
Critical Temperature (Tc): It is defined as that temperature above which a gas cannot be liquified however high pressure may be applied on the gas.
Tc = 8a/27bR
(Where a and b are van der Waals constants)
Critical Pressure (Pc): It is the pressure required to Liquify the gas at the critical temperature.
Pc = a/27b2
The volume occupied by one mole of the gas at the critical temperature and the critical pressure is called the critical volume (Vc).
For Example. For C02 to Liquify.
Tc = 30.98°C
Pc = 73,9 atm.
Vc = 95-6 cm3/mole
All the three are collectively called critical constants.
11. LIQUID STATE
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
LIQUID STATE
Characteristics of Liquid State
(i) In liquid, intermolecular forces are strong in comparison to gas.
(ii) They have definite volume but irregular shapes or we can say that they can take the shape of the container.
(iii) Molecules of liquids are held together by attractive intermolecular forces.
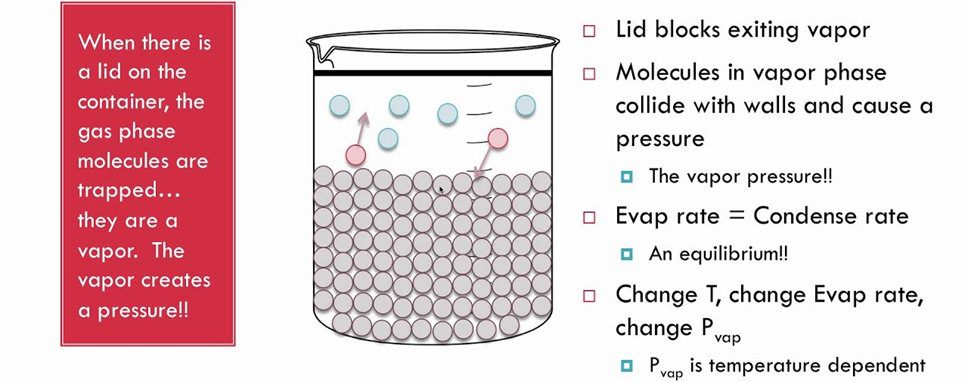
Vapour Pressure: The pressure exerted by the vapour of a liquid, at a particular temperature in a state of dynamic equilibrium, is called the vapour pressure of that liquid at that temperature.
Vapour Pressure depends upon two factors:
(i) Nature of Liquid
(ii) Temperature
• Surface Tension
It is defined as the force acting per unit length perpendicular to the line drawn on the surface of liquid.
S.I. unit of Surface Tension = Nm-1
Surface Tension decreases with increase in temperature, because force acting per unit length decreases due to increase in kinetic energy of molecules.
• Viscosity
It is defined as the internal resistance to flow possessed by a liquid.
The liquids which flow slowly have very high internal resistance, which is due to strong intermolecular forces and hence are said to be more viscous.
This force is proportional to the area of contact of layers and velocity gradient
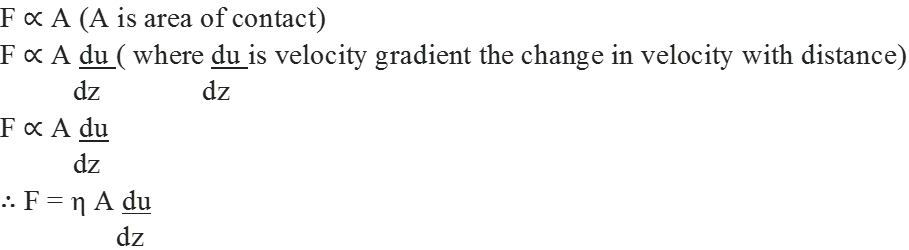
where ‘ η’ is proportionality constant and is called coefficient of viscosity. It is expressed in Nm-2s or poise
1 poise = 0.1 Nm-2s
When liquid flows, the layer immediately below it tries to retard its flow while the one above tries to accelerate.
Thus, force is required to maintain the flow of layers.

Effect of Temp, on Viscosity: Viscosity of liquids decreases as the temperature rises because at high temperature, molecules have high kinetic energy and can overcome the intermolecular forces to slip past one another.

 Ritan Sheth
Ritan Sheth
