Motivate the area of a circle;

Introduction :

We already know about the perimeter and areas of some simple figures like rectangle, square, rhombus, parallelogram etc. In this chapter, we shall learn how to find the perimeter and areas related to circular figures and we wiIl apply this knowledge to find the areas of some special parts of a circular region like sector, segment and combinations of plane figures.

Circle and its related Terms : 
Circle:    A circle is a collection of all points in a plane which are at a constant distance from a fixed point in the same plane.
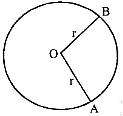
Radius:  A line segment joining the centre of the circle to a point on the circle is called its radius.
In Figure, there is a circle with centre O and its radius is OA. The length of the radius of a circle is generally denoted by the letter 'r'. 

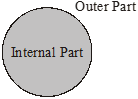
Internal and Outer Part :
A closed geometric figure in the plane divides the plane into three parts namely, the inner part of the figure, the figure and the outer part. In Figure the shaded portion is the inner part of the circle, the boundary is the circle and the unshaded portion is the outer part of the circle.

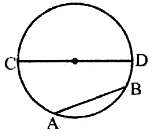
Chord: A line segment joining any two points of a circle is called a chord. A chord passing though the centre of circle is called its diameter. AB and CD both are chords but the chord CD passes through the centre. 
Hence CD is the diameter also.
Diameter of a circle = twice the radius of the circle.                
Note: Diameter is the longest chord of a circle.
Arc: A part of a circle is called an arc.

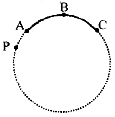
Semicircle: A diameter of a circle divides a circle into two equal arcs, each known as a semicircle. In Figure, PQ is a diameter and arc PRQ is a semicircle and so is arc PBQ.

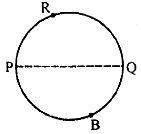
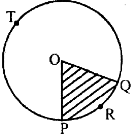
Sector: The region bounded by an arc of a circle and two radii at its end points is called a sector. In the figure, the shaded portion is a sector formed by the arc PRQ and the unshaded portion is a sector formed by the arc PTQ.

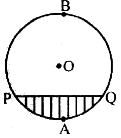
Segment: A chord divides the interior of  a circle into two parts, each called a segment. The segment in which the centre of the circle does not lie is called minor segment and the segment in which the centre of the circle lies is called major segment. In the figure, the shaded region PAQP and the unshaded region PBQP are both segments of the circle. PAQP is called a minor segment and PBQP is called a major segment.

Perimeter and Area of a Circle -A Review

 

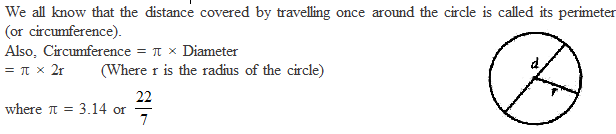
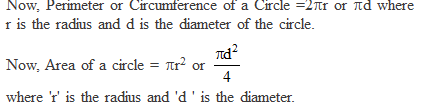
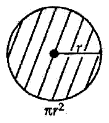
Problems on finding surface areas and volumes of combinations of any two of the following: cubes, cuboids, spheres, hemispheres and right circular cylinders/cones. Frustum of a cone.

INTRODUCTION 
    In our day-to-day life we come across various solids which are combinations of two or more such solids. 
    We shall discuss problems on finding surface areas and volumes of such solids. 
    Before we proceed further let us recall the formulas for surface area and volume of some of the basic solids:

Right circular cylinder: For a right circular cylinder of base radius r and height h, we have -

 

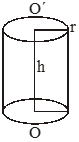
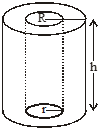Right circular cone: For a right circular cone of height h, slant height 
    l and radius of base r, we have,
    (i)     l2 = r2 + h2
    (ii)     Curved surface area = p r l sq units                    
    (iii)     Total surface area
            = Curved surface area + area of the base

 

 

 

 

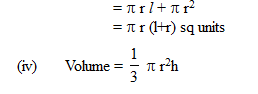
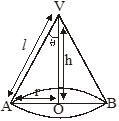
Illustration 1
     The dimensions of a metallic cuboid are 100 cm x 80 cm ´ 64 cm. It is melted and recast into a cube. Find the surface area of the cube.
  Solution
            We have 
            Volume of the metallic cuboid = 100  x 80 x 64 cm3 = 512000 cm3.
            Since the metallic cuboid is melted and is recast into a cube.
            Volume of the metallic cuboid = Volume of the cube.
            Let the length of each edge of the recasted cube be a cm, then,
            Volume of cube = Volume of the cuboid
            a3 = 512000
            a3 = 83 x 103 
            a = 8 x 10 cm = 80 cm

             Surface area of the cube = 6a2  cm2  = 6 x  (80)2 cm2 = 38400 cm2

 Illustration 2
            The radii of the bases of two right circular solid cones of same height are r1 and  r2 respectively. The cones are melted and recast into a solid sphere of radius R.

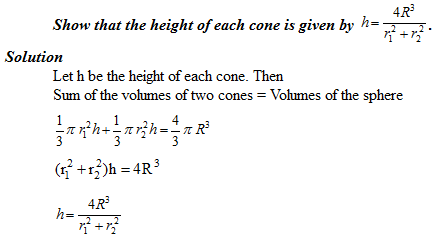
area of sectors and segments of a circle.

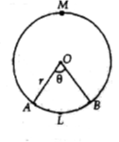
Areas of Sector and Segment of a Circle :
We know that, the circular region enclosed by two radii and the corresponding arc is called 'a sector of the circle' and the circular region enclosed by the chord and corresponding arc is called a segment of the circle. There are two types of sector and segment each in a circle.

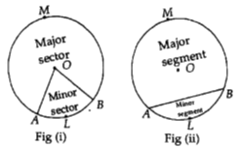
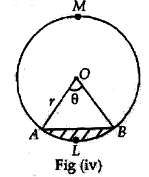
Major sector: It is the sector of a circle in which major arc is the part of its boundary. In the given fig.(i) OAMB is the major sector.
Minor sector : It is the sector of a circle in which minor arc is the part of its boundary. In the given fig. (i) OALB is the minor sector.
Minor segment: It is the segment of a circle in which minor arc is the part of its boundary. In the given fig.(ii) ALB is the minor segment.

 

area of sectors and segments of a circle.

note in Chapter 1. AREAS RELATED TO CIRCLES > area of sectors and segments of a circle.

Problems based on areas mfand perimeter / circuerence of the above said plane figures.

this is manas

Problems involving converting one type of metallic solid into another and other mixed problems.

Surface area and volume of combination of solids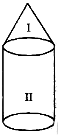      
    In this section we shall find the surface area and volume of solids which are combination of two or more solids.
    Consider a circus tent shown in the given figure.
    It consists of two parts I and II. Part-I is in the shape of a cone and Part-II is in the form of a cylinder.                                                               
    Total surface area of the circus tent = Curved surface area of part-I i.e., cone + Curved Surface area of part-II i.e., Cylinder.

Illustration 6
   A solid is composed of a cylinder with hemispherical ends. If the whole length of the  solid is 104 cm and the radius of each hemispherical end is 7         cm, find the

Solution : 
      The whole length of the solid = 104 cm
      The radius of each hemisphere = 7 cm
      Therefore, the length of the cylindrical part of the solid = (104 – 2 x 7) cm = 90 cm  Now, the total surface area of the solid 
     = 2 x (curved surface area of hemisphere) + (curved surface area of cylindrical part)

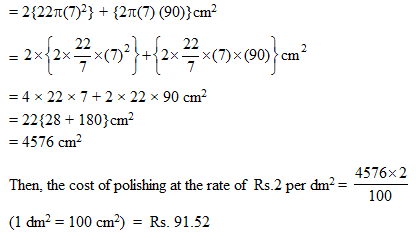
Volume of Combination of Solids :
 In the previous section, we have studied about the surface area of solids made of two or more solids. There we find that while calculating the surface area of a solid, some surface areas are not included. But, here we will find the total volume of a solid which is also the actual volume of two or more combined solid.

Illustration 7
 A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take p = 3.14)

Solution : 
Let BPC be the hemisphere and ABC be the cone standing on the base of the hemisphere

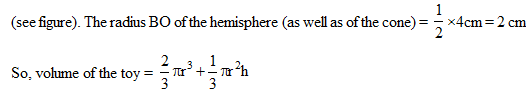
Conversion of Solid from One Shape to Another
    Some solids like candle, clay etc. can be changed into any shape. But the volume of the both solid shapes are same. For example, if a candle which is generally in the shape of a cylinder can be changed into any shape, but the volume remains same.
    If a solid is transformed into a number of small identical solids of same or a different shape, then 

 

Related Unit Name

Unit 1 Number Systems