Definitions, examples, counter examples of similar triangles.
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
A, B and C are three identical bulbs, which of the following change occurs in the brightness of bulb, when switch S is closed
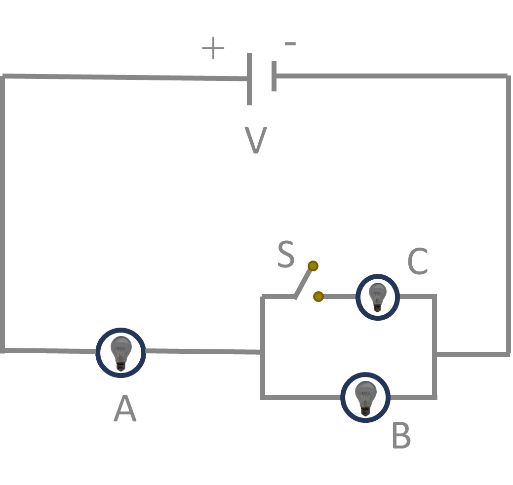
(a) A remains same, then B decreases
(b) A increases then B decreases
(c) A increases then B remains same
(d) A decreases then B increases
Definitions, examples, counter examples of similar triangles.
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
5.1 INTRODUCTION
In previous classes, we have learnt about the congruency of two geometric figures. In this chapter we shall learn about these geometric figures. Which have the same shape but not necessary have the same size. These kind of geometric figures are known as similar figures. So the congruent figures are always similar figures but similar figures need not be congruent figures.
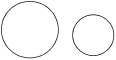
(i) Two line segments are similar

(The two line segments are congruent if they have the same length)
(ii) Two circles are similar.
(The two circles are congruent. If they have the same radius)
5.2 similar Polygons
Two polygons of the same number of sides are said to be similar. If
(i) Their corresponding angles are equal
(ii) Their corresponding sides are in the same ratio



Tangents to a circle motivated by chords drawn from points coming closer and closer to the point.
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
INTRODUCTION
In class IX, we have discussed about the circle and its centre and radius. Recall that a circle is a collection of all the points in a plane which are at a constant distance (called as radius) from a fixed point (called as centre). We have further studied about the chord, the segment, the sector, an arc etc. related to a circle. In this chapter, we shall discuss about the tangent to a circle and its properties. [The word tangent comes from the Latin word “tangere” which means to touch. It was introduced by the Danish Mathematician Thomas Fimeke in 1583.]
circle
A circle is a set of all the points in a plane which are at a constant distance from the fixed point. The fixed point is called the centre of the circle and the constant distance is called the radius of the circle.
A circle with centre at O and radius = r is generally written as C(O, r).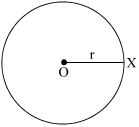
A line segment formed by joining the two points on the circle and passing through the centre of circle is called the diameter of the circle.
Secant
A line which intersects a circle in two distinct points is called a secant of the circle. PQ is a line which intersects a circle in two distinct points A and B. PQ is a secant.
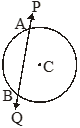
Tangent To a circle
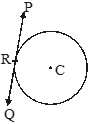
A tangent to a circle is a line that intersects the circle at only one point. In figure PQ is a tangent to a circle and R is called the point of contact of the tangent. The point of intersection of the circle and a tangent to it is known as point of contact.
Number of Tangents from a point on a circle
Case–I: There is no tangent to a circle passing through a point lying inside the circle.
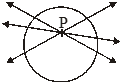
Case–II: There is one and only one tangent to a circle passing through a point lying on the circle.
Two circles and their common tangents
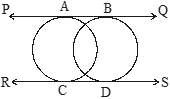
Case-I: When circles intersect in two points:
In this case, there will be two common tangents PQ and RS to the two circles as shown in figure.
Some properties of Tangent to a Circle
Theorem : 1
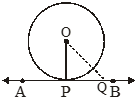
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Proof: Let AB be a tangent to the circle with centre O at the point P as shown in the figure. Join OP. We have to prove that OP is perpendicular to AB or AB is perpendicular to OP.
Take a point Q on AB other than the point P. Join OQ. If the point Q lies inside or on the circle, then the line PQ will intersect the circle in two different points and hence a secant.
Which contradicts the tangency of the line.
Therefore, the line Q lies outside the circle.
⟹ OQ is greater than the radius OP, i.e. OQ > OP. Since it happens for every point on the line AB except the point P.
Therefore, out of all the line segments joining the centre to any point on the line AB, the line segment OP is the shortest one.
As we know that among all the line segments joining the point O to a point on the line AB, the shortest one is perpendicular to the line AB.
Theorem : 2
A line drawn through the end point of a radius and perpendicular to it is a tangent to the circle.

Proof: Let AB be a line perpendicular to the radius OP of a circle with centre at O as shown in the figure.
Take a point Q other than P on the line AB. Since OP is perpendicular to the line AB.
Out of all the line segments joining O to a point on the line AB, OP is the shortest one.
So, OP < OQ or OQ > OP
The point Q lies exterior to (or outside) the circle.
Every point other than P on the line AB is an exterior point of the circle.
The line AB meets the circle at only one point P.
Hence, the line AB is a tangent to the circle at the point P.
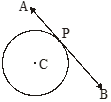
Length of Tangent
The length of the segment to the tangent between the point and the given points of contact with the circle is called the length of the tangent from the point to the circle. In figure PT and PT’ are the lengths of tangents from point P to the circle.
Normal to a Circle : The line containing the radius through the point of contact is known as the normal to the circle at the point of contact.
IMPORTANT RESULTS FOR CIRCLE AND TANGENTS TO A CIRCLE
1. One and only one tangent can be drawn at any point on the circle.
2. If PAB is a secant to a circle intersecting it at A and B and PT is a tangent, then PA × PB = PT2.
3. The points of intersection of direct common tangents and transverse common tangents to two circles divide the line segment joining the two centres externally and internally respectively in the ratio of their radii.
4. If two chords AB and CD of a circle intersect each other at P outside the circle, then PA ´ PB = PC ´ PD.
Division of a line segment in a given ratio (internally)
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
INTRODUCTION
In previous classes, we have studided certain constructions using a ruler and a compass. There are : bisecting an angle, drawing the perpendicular bisector of a line segment, construction of some triangle, etc. We have also given their justifications. Here, we shall study some more constructions taking into use the above pervious knowledge. Also, we shall give mathematical reasoning underlying these constructions.
Divison of A line segment :
In order to divide a line segment internally in a given ratio m : n, where both m and n are positive integers, we follow the following steps :
Steps of construction :
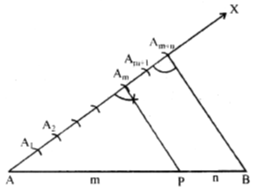
(i) Draw a line segment AB of given length by using a ruler.
(ii) Draw any ray AX making a suitable acute angle with AB.
(iii) Along AX draw (m + n) arcs intersecting the rays AX at A1, A2 ............, Am, Am+1, ........., Am + n such that AA1 = A1A2 =...............= Am+n–1 Am+n
(iv) Join B Am+n
(v) Through the point Am draw a line parallel to Am+n B by making ∠AAm P = ∠AAm+n B.
Suppose this line meets AB at point P.
The point P so obtained is the required point which divides AB internally in the ratio m : n.
Illustration
Divide a line segment of length 12 cm internally in the ratio 3 : 2.
Solution
Steps of construction :
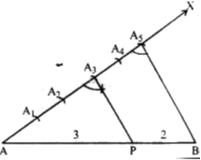
(i) Draw a line segment AB = 12 cm by using a ruler.
(ii) Draw a ray making a suitable acute angle ∠BAX with AB.
(iii) Along AX, draw 5 ( = 3 + 2) arcs intersecting the rays AX at A1, A2, A3, A4 and A5 such that
AA1 = A1A2 = A2A3 = A3A4 = A4A5
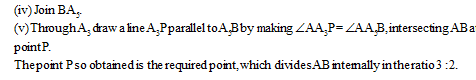
Tangent to a circle from a point outside it?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
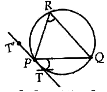
Construction of a Tangent to a Circle at a given point when its centre is not known :
Steps of construction :
Draw a circle of radius r cm.
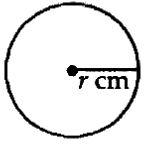
Mark a point P on it. Draw any chord PQ.
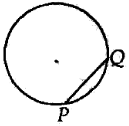
Take a point R on the major arc QP. Join RP & RQ.
Produce TP to T" such that T' PT is the required tangent at P.
Construction of Tangent to a Circle from a Point Outside it when the Centre of the Circle is
known :
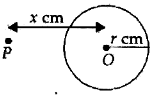
Steps of Construction :
Draw a circle with O as centre and radius r cm. Mark a point P outside the circle such that OP = x cm.
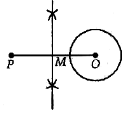
Join OP and draw its perpendicular bisector, which cut OP at M.
Steps of Construction :
Draw a circle with O as centre and radius r cm and any diameter AOB of this circle.
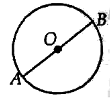
Construct the given angle at O such that radius OC meets the circle at C. (Suppose given angle is 90º)
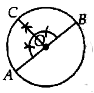
Draw perpendicular at A and C intersect each other at P.
Hence PA and PC are the required tangents to the given circle, inclined at a given angle.
Construction of a triangle similar to a given triangle?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
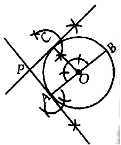
Constructions of A triangle similar to a given triangle :
Scale factor :
The ratio m : n of the side of the triangle to be constructed with the corresponding sides of the given triangle is known as their scale factor.
(I) Steps of construction when m < n :
(i) Construct the given triangle ABC by using the given data.
(ii) Take any one of the three side of the given triangle as base. Let AB be the base of the given triangle.
(iii) At one end, say A, of the base AB below the base AB, draw a ray AX making a suitable acute angle with AB below the base AB.
(iv) Along AX mark n point A1, A2, A3, ............, An such that
AA1 = A1A2 = ..............An–1An.
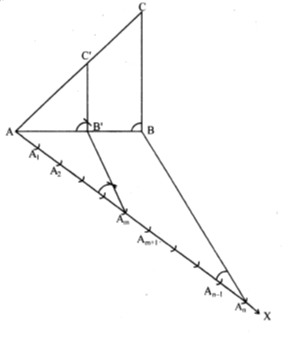
Illustration 1
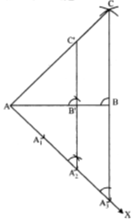
Construct a ∆ABC in which AB = 5 cm, BC = 6 cm and AC = 7 cm. Now, construct a triangle similar to ∆ABC such that each of its sides is two-third of the corresponding sides of ∆ABC.
Solution :
Steps of construction :
(i) Draw a line segment AB = 5 cm.
(ii) With A as centre and radius = 7 cm, draw an arc above AB.
(iii) With B as centre and radius = 6 cm, draw another arc, inter
secting the arc drawn in step (ii) at C.
(iv) Join AC and BC to obtain DABC.
(v) Below AB, draw a ray AX making a suitable acute angle with AB on opposite side of C with respect to AB.
(vi) Draw three arcs (greater of 2 and 3 in 2/3) intersecting the ray AX at A1, A2, A3 such that
AA1 = A1A2 = A2A3


(iv) Draw arcs (large of m and n) intersecting the ray AX at A1, A2, A3 , ..........., Am such that AA1 = A1A2 = ........... = Amm–1 Am.
(v) Join An to B.
(vi) Draw a line through Am parallel to AnB, intersecting the extended line segment AB at B.
(vii) Draw a line through B¢ parallel to BC intersecting the extended line segment AC at C.
(viii) ∆ABCso obtained is the required triangle.

 Carrier Point
Carrier Point
