- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Illustration : 1
A box contains 3 blue, 2 white and 4 red marbles. If a marble is drawn at random from the box, what is the probability that it will be
(i) white ? (ii) blue ? (iii) Red ?
Solution :
Saying that a marble is drawn at random is a short way of saying that all the marbles are equally likely to be drawn.
Therefore, the number of possible outcomes = 3 + 2 + 4 = 9
Let W denote the event ‘the marble is white’ , B denotes the event ‘the marble is blue’ and R denote the event ‘marble is red’.

Illustration : 2
Two coins are tossed simultaneously. Find the probability of getting
(i) two heads (ii) at least one head (iii) no head.
Solution :
Let H denotes head and T denotes tail.
On tossing two coins simultaneously, all possible outcomes HH, HT, TH, TT = 4.
![]()

Illustration : 3
17 cards numbered 1, 2, 3, ........, 17 are put in a box and mixed throughly. One person draws a card from the box. Find the probability that the number on the card is
(i) odd (ii) a prime (iii) divisible by 3 (iv) divisible by 3 and 2 both.
Solution :
(i) There are 9 odd numbered cards, namely 1, 3, 5, 7, 9, 11, 13, 15, 17. Out of these 9 cards one card can be drawn in 9 ways.
Favourable number of elementary events = 9
Total number of elementary events = 17.
![]()
(ii) There are 7 prime numbered cards, namely. 2, 3, 5, 7, 11, 13, 17. Out of these 7 cards one card can be chosen in 7 ways.
Favourable number of elementary events = 7
Total number of elementary events = 17
.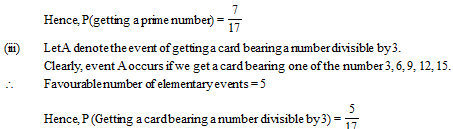
(iv) If a number is divisible by both 3 and 2, then it is a multiple of 6. In cards bearing number 1, 2, 3, ........17 there are only 2 cards which bear a number divisible by 3 and 2 both i.e., by 6. These cards bear numbers 6 and 12.
Favourable number of elementary events = 2
![]()


 Param Publication
Param Publication
