- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
INTRODUCTION
In our day-to-day life we come across various solids which are combinations of two or more such solids.
We shall discuss problems on finding surface areas and volumes of such solids.
Before we proceed further let us recall the formulas for surface area and volume of some of the basic solids:

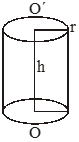
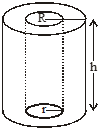
Right circular cylinder: For a right circular cylinder of base radius r and height h, we have -

 Right circular cone: For a right circular cone of height h, slant height
Right circular cone: For a right circular cone of height h, slant height
l and radius of base r, we have,
(i) l2 = r2 + h2
(ii) Curved surface area = p r l sq units
(iii) Total surface area
= Curved surface area + area of the base
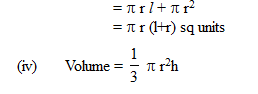
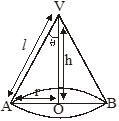
Illustration 1
The dimensions of a metallic cuboid are 100 cm x 80 cm ´ 64 cm. It is melted and recast into a cube. Find the surface area of the cube.
Solution
We have
Volume of the metallic cuboid = 100 x 80 x 64 cm3 = 512000 cm3.
Since the metallic cuboid is melted and is recast into a cube.
Volume of the metallic cuboid = Volume of the cube.
Let the length of each edge of the recasted cube be a cm, then,
Volume of cube = Volume of the cuboid
a3 = 512000
a3 = 83 x 103
a = 8 x 10 cm = 80 cm
Surface area of the cube = 6a2 cm2 = 6 x (80)2 cm2 = 38400 cm2
Illustration 2
The radii of the bases of two right circular solid cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R.
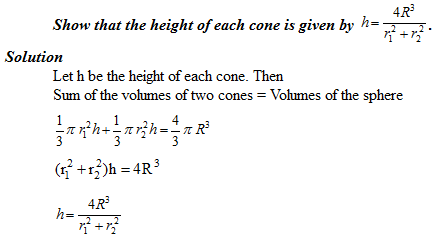

 Param Publication
Param Publication
