- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Surface area and volume of combination of solids 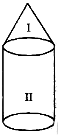
In this section we shall find the surface area and volume of solids which are combination of two or more solids.
Consider a circus tent shown in the given figure.
It consists of two parts I and II. Part-I is in the shape of a cone and Part-II is in the form of a cylinder.
Total surface area of the circus tent = Curved surface area of part-I i.e., cone + Curved Surface area of part-II i.e., Cylinder.
Illustration 6
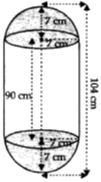
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the
![]()
Solution :
The whole length of the solid = 104 cm
The radius of each hemisphere = 7 cm
Therefore, the length of the cylindrical part of the solid = (104 – 2 x 7) cm = 90 cm Now, the total surface area of the solid
= 2 x (curved surface area of hemisphere) + (curved surface area of cylindrical part)
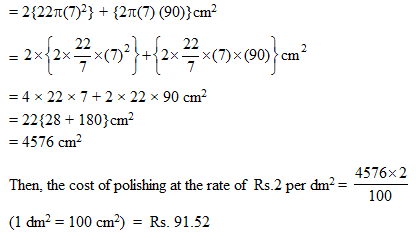
Volume of Combination of Solids :
In the previous section, we have studied about the surface area of solids made of two or more solids. There we find that while calculating the surface area of a solid, some surface areas are not included. But, here we will find the total volume of a solid which is also the actual volume of two or more combined solid.
Illustration 7
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take p = 3.14)
Solution :
Let BPC be the hemisphere and ABC be the cone standing on the base of the hemisphere
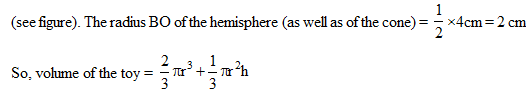

Conversion of Solid from One Shape to Another
Some solids like candle, clay etc. can be changed into any shape. But the volume of the both solid shapes are same. For example, if a candle which is generally in the shape of a cylinder can be changed into any shape, but the volume remains same.
If a solid is transformed into a number of small identical solids of same or a different shape, then
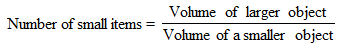


 Param Publication
Param Publication
