- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
INTRODUCTION :
In practical life, we must have observed many things follow a certain pattern, such as the petals of a sunflower, the holes of a honeycomb, the grains on a maize cob, the spirals on a pineapple on a pipe cone.
In our day-to-day life we see patterns of geometric figures on clothes, picture, posters. They make the learners motivated to form such new pattern.
For example,

Likewise number patterns are also faced by learners. In their study, number pattern play an important role in the field of mathematics.
Ex. (i) 2, 4, 6, 8, 10 then next number is 12.
![]()
Idea on A.P. was given by mathematician Carl Friedrich Gauss, who was a young boy, stunned his teacher by adding up 1 + 2 + 3 + ........+ 99 + 100 within a few minutes. Here’s how he did it:
He realised that adding the first and last numbers, 1 and 100, gives, 101; and adding the second and second last numbers, 2 and 99, gives 101, as well as 3 + 98 = 101 so on .
Thus he concluded that there are 50 sets of 101. So the series is :
50(1 + 100) = 5050.
In this chapter, you will study only Arithmetic Progression (A.P.) and Geometric Progression (G.P.).
Arithmetic progression (A.P.) :
A sequence is called an arithmetic progression, if the difference of a term and previous term is always same.
The difference is called the common difference of arithmetic progression.
The sequence is called an arithmetic progression (A.P.), if d = x2 – x1 = x3 – x2 = xn – xn – 1 = ...........
It is a sequence whose terms decrease or increase by a fix/constant number. This constant number is called common difference of A.P. and it generally denoted by ‘d’.
[d = an+1–an]
Illustration 1
Find the A.P. whose 1st term is 2 & common difference is 3.
Solution
Given : First term (a) = 2 & Common difference (d) = 3.
A.P. is 2, 5, 8, 11, 14,.......
Illustration 2
Show that the sequence on defined by an = 4n + 5 is an A.P. Also find its common difference.
Solution
a1 = 9, a2 = 13, a3 = 17,....... in A.P.
We have an = 4n + 5 .....(i)
Replacing n by (n + 1) we get
an +1 = 4(n + 1) + 5 = 4n + 4 + 5
an+1 = 4n + 9 .....(ii)
d = an+1 – an ⟹ d = (4n + 9) – (4n + 5) ⟹ d = 4
Remarks:
(i) The common difference ‘d’ should be independent of n.
Properties of Arithmetic Progression :
Property–1: If a constant is added to or subtracted from each term of an AP, then the resulting sequence is also an AP with the same common difference.
Property–2: If each term of a given AP is multiplied or divided by a non-zero constant k, then the resulting sequence is also an AP with common difference kd or d/k respectively. Where d is the common difference of the given AP.
Property–3: In a finite AP the sum of the terms equidistant from the beginning and end is always same and is equal to the sum of first and last term i.e. ak + an – (k – 1) = a1 + an For all k = 1, 2, 3........(n – 1)
Property–4: Three numbers a, b, c are in AP if 2b = a + c
Property–5: A sequence is an AP if its nth term is a linear expression in n i.e. an = An + B where A, B are constants. In such a case the coefficient of n in an is the common difference of the AP.
Property–6: A sequence is an AP if the sum of its first n terms is of the form An2 + Bn where A, B are constants independent of n. In such a cases the common difference is 2A. i.e. 2 times the coefficient of n2.
Property–7: If the terms of an AP are chosen at regular intervals then they form an AP.
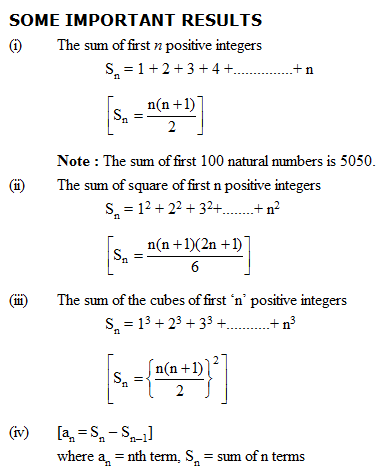

 Carrier Point
Carrier Point
