- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Introduction :
We already know about the perimeter and areas of some simple figures like rectangle, square, rhombus, parallelogram etc. In this chapter, we shall learn how to find the perimeter and areas related to circular figures and we wiIl apply this knowledge to find the areas of some special parts of a circular region like sector, segment and combinations of plane figures.
Circle and its related Terms :
Circle: A circle is a collection of all points in a plane which are at a constant distance from a fixed point in the same plane.
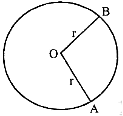
Radius: A line segment joining the centre of the circle to a point on the circle is called its radius.
In Figure, there is a circle with centre O and its radius is OA. The length of the radius of a circle is generally denoted by the letter 'r'.
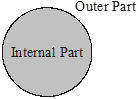
Internal and Outer Part :
A closed geometric figure in the plane divides the plane into three parts namely, the inner part of the figure, the figure and the outer part. In Figure the shaded portion is the inner part of the circle, the boundary is the circle and the unshaded portion is the outer part of the circle.
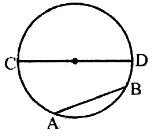
Chord: A line segment joining any two points of a circle is called a chord. A chord passing though the centre of circle is called its diameter. AB and CD both are chords but the chord CD passes through the centre.
Hence CD is the diameter also.
Diameter of a circle = twice the radius of the circle.
Note: Diameter is the longest chord of a circle.
Arc: A part of a circle is called an arc.
![]()
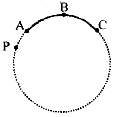
Semicircle: A diameter of a circle divides a circle into two equal arcs, each known as a semicircle. In Figure, PQ is a diameter and arc PRQ is a semicircle and so is arc PBQ.
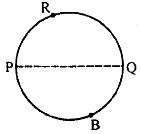
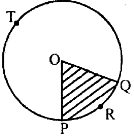
Sector: The region bounded by an arc of a circle and two radii at its end points is called a sector. In the figure, the shaded portion is a sector formed by the arc PRQ and the unshaded portion is a sector formed by the arc PTQ.
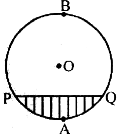
Segment: A chord divides the interior of a circle into two parts, each called a segment. The segment in which the centre of the circle does not lie is called minor segment and the segment in which the centre of the circle lies is called major segment. In the figure, the shaded region PAQP and the unshaded region PBQP are both segments of the circle. PAQP is called a minor segment and PBQP is called a major segment.
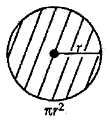
Perimeter and Area of a Circle -A Review
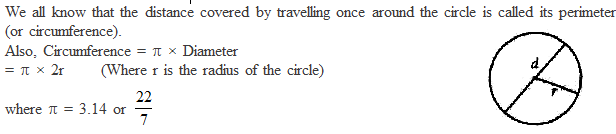
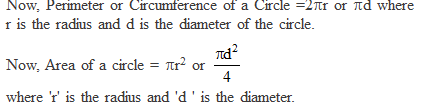

 Param Publication
Param Publication
