2.Arithmetic Fundamental Theorem

Prime Factorisation of Numbers Using Fundamental Theorem of Arithmetic

We know that all composite numbers can be represented as the product of two or more prime numbers. Let us understand this concept by taking the example of 36 and factorising it in different ways.

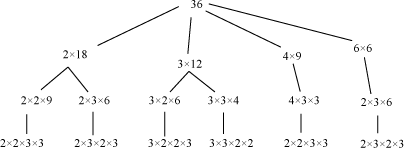
We can see that whichever way we factorise the number 36, it will be broken down as the product of the same prime numbers, which is unique. The only difference is that the ordering of the prime numbers will be different for different ways of factorising the number. In fact, this is true for all numbers. We can check this by taking the example of a larger number, say 21560, which can be uniquely broken down into its prime factors as

2³ × 5 × 7² × 11

Hence, we can say that any composite number can be written in the form of the product of prime numbers, which is unique, except the order in which they occur. By this, we mean that 2 × 3 × 7 × 11 is the same as 7 × 11 × 2 × 3.

This is the fundamental theorem of arithmetic. It can be formally stated as:

Thus, this theorem can be used to write the prime factorisation of any number. Let us try to build on this concept with the help of some examples.

Example 1:

Write the prime factorization of 31250. What are its prime factors? Solution:

31250 = 2 × 15625

= 2 × 5 × 3125

= 2 × 5 × 5 × 625

= 2 × 5 × 5 × 5 × 125

= 2 × 5 × 5 × 5 × 5 × 25

= 2 × 5 × 5 × 5 × 5 × 5 × 5

= 2 × 5⁶

Hence, 2 × 5⁶ is the prime factorisation of 31250. Its prime factors are 2 and 5.

Example 2: If it is given that 13125 = 2^a ×3^b× 5^c× 7^d, then find the value of a +2b +7c + 11d.

Solution:

2^a × 3^b × 5^c × 7^d = 13125

= 3 × 4375

= 3 × 5 × 875

= 3 × 5 × 5 ×175

= 3 × 5 × 5 × 5 × 35

= 3 × 5 × 5 × 5 × 5 × 7

= 3¹ × 54 × 7¹

∴ 2^a × 3^b × 5^c × 7^d = 2⁰ × 3¹ × 5⁴ × 7¹

Comparing exponents of the bases (integers): a = 0, b = 1, c = 4, and d =1

Hence, a +2b +7c +11d = 0 + 2 ×1 + 7 × 4 + 11 × 1

= 0 + 2 + 28 + 11

= 41

Example 3: Show that the expressions given below are composite numbers.

(a) 3 × 5 × 7 × 23 + 2 × 7 × 11 × 13

(b) 29 × 35 + 14

(c) 3⁴ + 6³

Solution:

(a) 3 × 5 × 7 × 23 + 2 × 7 × 11 × 13 = 7( 3 × 5 × 23 + 2 × 11 × 13)

= 7(345 + 286)

= 7 × 631

Since both 7 and 631 are prime numbers, we have expressed the given expression as the product of two prime numbers. We know that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.

(b) 29 × 35 + 14 = 29 × 5 × 7 + 2 × 7

= 7(29 × 5 + 2)

= 7 × 147

= 7 × 3 × 7 × 7

= 3 × 7³

Since both 3 and 7 are prime numbers, we have expressed the given expression as the product of its prime factors. We know that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.

(c) 3⁴ + 6³ = 3⁴ + (2 × 3) ³

= 3⁴ + 2³ × 3³

= 3³(3 + 2³)

= 3³ × 11

Since both 3 and 11 are prime numbers, we have expressed the given expression as the product of its prime factors. It is known that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.

Application Of The Fundamental Theorem Of Arithmetic To Find The HCF And LCM Of Numbers

All composite numbers can be written as the product of two or more prime numbers. For example, 20 can be written as 2² × 5; 54 can be written as 2 × 3³, and so on.

Note that if we do not consider the way in which the prime factors are written, then we can prime factorise every number in only one way. This applies to other numbers as well.

This leads to the fundamental theorem of arithmetic, which states that:

Even though we did not notice it before, whenever we prime factorise a number, we use the fundamental theorem of arithmetic to do so.

For example, the prime factorisation of 980 is represented as

980 = 2 × 490

= 2 × 2 × 245

= 2 × 2 × 5 × 49

= 2 × 2 × 5 × 7 × 7

= 2² × 5¹ × 7²

Hence, 2² × 5¹ × 7² is the prime factorisation of 980; and 2, 5, and 7 are its prime factors.

By applying the fundamental theorem of arithmetic to the prime factorized numbers, we can also find their HCF and LCM.

This is known as the prime factorisation method, which states that:

Let us understand this method with the help of some examples.

Example 1: Find the LCM and the HCF of 432 and 676 using the prime factorization method.

Solution:

We can write these numbers as

432 = 24 × 3³

676 = 2² × 13²

To calculate the HCF

We observe that the only common prime factor is 2 and the smallest power of this prime factor is also 2.

Thus, HCF (432, 676) = 2² = 4

To calculate the LCM

We observe that the prime factors of 432 and 676 are 2, 3, and 13. The greatest powers of these factors are 4, 3, and 2 respectively.

LCM is the product of the greatest power of each prime factor.

Thus, LCM (432, 676) = 2⁴ × 3³ × 13² = 73008

Example 2: Find the HCF and the LCM of 28, 42, and 64 using the prime factorization method.

Solution:

We can write these numbers as

28 = 2² × 7¹

42 = 2 × 3¹ × 7¹

64 = 2⁶

HCF is the product of the smallest power of each common prime factor. Here, the only common prime factor is 2 and its power is 1.

Thus, HCF (28, 42, 64) = 2¹ = 2

LCM is the product of the greatest power of each prime factor. Thus, LCM (28, 42, 64) = 2⁶ × 3¹ × 7¹ = 1344

Example 3: Find the HCF and the LCM of 1080 and 900 using the prime factorization and show that HCF × LCM = Product of two numbers.

Solution:

1080 = 2³ × 3³ × 5

900 = 2² × 3² × 5²

Hence, HCF (1080, 900) = 2² × 3² × 5 = 180

LCM (1080, 900) = 2³ × 3³ × 5² = 5400

HCF × LCM = 180 × 5400 = 972000

Product of numbers = 1080 × 900 = 972000

Hence, HCF × LCM = Product of two numbers

Example 4: The HCF of 273 and another number is 7, while their LCM is 3003. Find the other number.

Solution:

Let the first number (a) be 273 and the second number be b.

It is given that HCF (a, b) = 7 and LCM (a, b) = 3003.

We know that HCF LCM = Product of two numbers.

⇒ HCF (a, b) × LCM (a, b) = a × b

⇒ 7 × 3003 = 273 × b

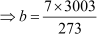
⇒ b = 77

Hence, the other number is 77.

Example 5: Anurag takes 6 minutes to complete one round of jogging around the circular track of a park, while Twinkle takes 8 minutes to do the same. If both of them start jogging at the same time from the same point, then how much time will they take before they meet at the point from which they started?

Solution:

Since Anurag and Twinkle take 6 minutes and 8 minutes respectively to complete one round of the circular track, the time after which they will meet at the starting point will be the lowest multiple of 6 and 8, i.e., their LCM.

6 = 2 × 3

8 = 2³

∴ LCM (6, 8) = 2³ × 3 = 24

Thus, they will meet at the starting point after 24 minutes.

Example 6: There are 120 students in a class. When the students were arranged according to their roll numbers, it was observed that every second student got distinction in Mathematics, every third student got distinction in Science, and every fifth student got distinction in English. How many students got distinction in all three subjects?

Solution:

As every second, third, and fifth student got distinction in Math, Science, and English respectively, the roll numbers of the students who got distinction in all three subjects will be equal to the multiples of the LCM of 2, 3, and 5.

LCM (2, 3, 5) = 2 × 3 × 5 = 30

Thus, every 30^th student got distinction in all three subjects.

Thus, a total of 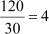students got distinction in all three subjects.

Properties Of Prime Numbers

Consider the number 8ⁿ, where n is a natural number.

Is there any value of n for which 8ⁿ ends with zero?

It is difficult to answer this question directly. However, we can answer this question by making use of the fundamental theorem of arithmetic. It states that

This means that if we are given a composite number, then that number can be written as a product of prime numbers in only one way (except for the order of prime numbers).

For example: the composite number 255 can be written as the product of primes as follows. 255 = 3 × 5 × 17

Also, 255 can be written as 3 × 17 × 5 or 5 × 3 × 17 or 5 × 17 × 3 or 17 × 3 × 5 or 17 × 5 × 3.

Thus, we can see that 255 can be expressed as a product of unique prime numbers 3, 5, and 17 but the order of representation may differ.

Now, by making use of the above theorem, we can answer the question which we were discussing in the beginning. Let us see how.

Suppose the number 8n ends with zero for some value of n. Since the number ends with zero, it should be divisible by 10. Now, 10 = 2 × 5

Thus, this number should be divisible by 2 and 5 also.

Therefore, the prime factorization of 8n should contain both the prime numbers 2 and 5. We have, 8ⁿ = (2³)ⁿ = 2³ⁿ

⇒ The only prime in the factorization of 8ⁿ is 2.

Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 8ⁿ.

Hence, there is no natural number n for which 8n ends with the digit zero. In this way, we can make use of the above theorem.

Let us now look at some more examples to understand this concept better.

Example 1: Prove that the number 9ⁿ, where n is a natural number, cannot end with a zero.

Solution:

Suppose the number 9ⁿ ends with a zero for some value of n.

Since the number ends with zero, it should be divisible by 10.

Now, 10 = 2 × 5

Thus, this number should be divisible by 2 and 5 also.

Therefore, the prime factorization of 9ⁿ should contain both the prime numbers 2 and 5.

We have, 9ⁿ = (32)ⁿ = 3²ⁿ

⇒ The only prime in the factorization of 9ⁿ is 3.

Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 9ⁿ.

Hence, there is no natural number n for which 9ⁿ ends with the digit zero.

Example 2: Check whether the numbers 49ⁿ, where n is a natural number, can end with a zero.

Solution:

Suppose the number 49n ends with a zero for some value of n.

Since the number ends with zero, it should be divisible by 10.

Now, 10 = 2 × 5

Thus, this number should be divisible by 2 and 5 also.

Therefore, the prime factorization of 49n should contain both the prime numbers 2 and 5. We have, 49ⁿ = (7²)ⁿ = 7²ⁿ

⇒ The only prime in the factorization of 49ⁿ is 7.

Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 49ⁿ.

Thus, there is no natural number n for which 49ⁿ ends with the digit zero.