- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
INTRODUCTION
In previous classes, we have studided certain constructions using a ruler and a compass. There are : bisecting an angle, drawing the perpendicular bisector of a line segment, construction of some triangle, etc. We have also given their justifications. Here, we shall study some more constructions taking into use the above pervious knowledge. Also, we shall give mathematical reasoning underlying these constructions.
Divison of A line segment :
In order to divide a line segment internally in a given ratio m : n, where both m and n are positive integers, we follow the following steps :
Steps of construction :
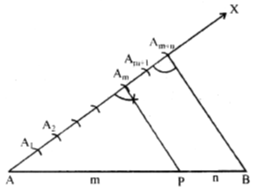
(i) Draw a line segment AB of given length by using a ruler.
(ii) Draw any ray AX making a suitable acute angle with AB.
(iii) Along AX draw (m + n) arcs intersecting the rays AX at A1, A2 ............, Am, Am+1, ........., Am + n such that AA1 = A1A2 =...............= Am+n–1 Am+n
(iv) Join B Am+n
(v) Through the point Am draw a line parallel to Am+n B by making ∠AAm P = ∠AAm+n B.
Suppose this line meets AB at point P.
The point P so obtained is the required point which divides AB internally in the ratio m : n.
Illustration
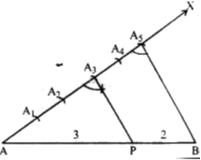
Divide a line segment of length 12 cm internally in the ratio 3 : 2.
Solution
Steps of construction :
(i) Draw a line segment AB = 12 cm by using a ruler.
(ii) Draw a ray making a suitable acute angle ∠BAX with AB.
(iii) Along AX, draw 5 ( = 3 + 2) arcs intersecting the rays AX at A1, A2, A3, A4 and A5 such that
AA1 = A1A2 = A2A3 = A3A4 = A4A5
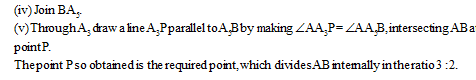

 Param Publication
Param Publication
