- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
6.12 GRAPHICAL REPRESENTATION :
Graphical Representation : Many types of graphs are employed in statistics, depending upon the nauture of the data involved. Among these are
(i) Bar chart (or Bar graph)
(ii) Histograms
(iii) Frequency Polygon
(iv) Cumulative Frequency Curve (Ogive)
(v) Pie chart (or Pie graph or Pie Diagrams)
Cumulative frequency Curve (Ogive) :
The term ‘ogive’ is pronounced as ‘ojeev’ and is derived from the word ogee. An ogee is a shape consisting of a concave arc flowing into a convex arc, so forming an S-shaped curve with vertical ends.
Note : For drawing ogives, it should be ensured that the class intervals are continuous. An ogive is the graphical representation of cumulative frequency distribution. We can construct two types of ogives. The first form is “less than ogive” and the second is “more than ogive”.
In the “less than” method we start with the upper limit of the classes and go on adding the frequencies. When these are plotted, we get a rising curve.
In the “more than” method we start with the lower limit of the classes and from the total frequencies we subtract the frequency of each class. When these are plotted, we get declining curve, e.g.
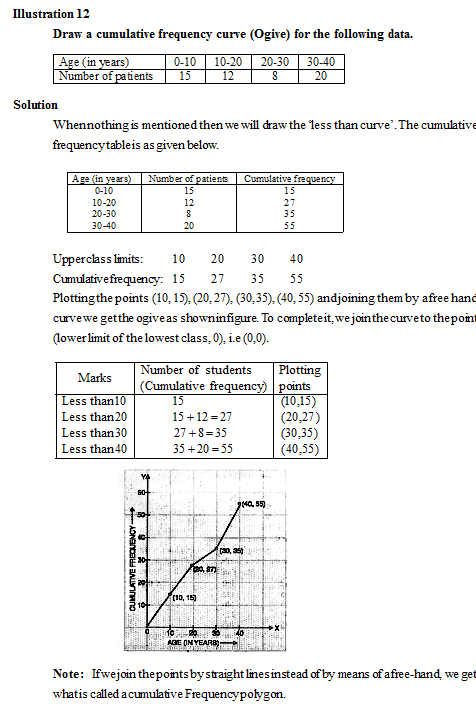
6.12.1 The less than method
In this method the Ogive is cumulated upward. Scale the cumulative frequencies along the y-axis, and exact upper limits along the x-axis. The scale along the y-axis should be such as may accommodate the total frequency.
Procedure:
Step–1: Form the cumulative frequency table.
Step–2: Mark the actual upper class limits along the x-axis.
Step–3: Mark the cumulative frequencies of respective classes along the y-axis.
Step–4: Plot the points (upper limits, corresponding cumulative frequency).
To complete the ogive we also plot the point (lower limit of the lowest class, 0).
Step–5: Join these points by a smooth curve.
The curve so obtained is the required ogive.

 Param Publication
Param Publication
