- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Introduction :
The chances of happening or non happening of an event when expressed quantitatively is called probability. There are mainly two definitions of probability.
(i) Experimental (ii) Theoretical
In this chapter, we will study about these two types of probability. Experimental probability approach is when we toss the coin one – million times or 10 million times, we observe that as the number of tosses increases the experimental probability of a head or a tail comes close to 0.5. This is experimental approach to probability. The basic difference between the experimental and theoretical approach to probability is that former is based on what has actually happened but later is based on prediction of what will happen
Probability – A Theoretical Approach
If an event A occurs m times and does not occurs n times. Then, the probability of occurence of event A, denoted by P(A) is given by

Sum of the Probabilities of All the Elementary Event of an Experiment
If E1 , E2 ..........., En be the n elementary events associated with a random experiment having exactly n outcomes, then P(E1) + P(E2) + .......... + P(En) = 1.
For example, when we toss a coin, the resulting elementary events are H and T.
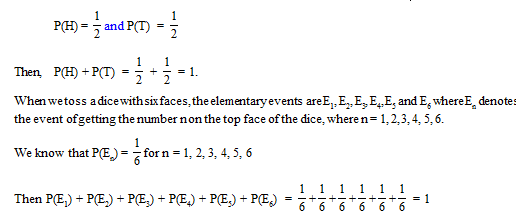

 Param Publication
Param Publication
