1.Zeros of Polynomial
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
CBSE Class 10 Maths Notes Chapter 2 Polynomials
- “Polynomial” comes from the word ‘Poly’ (Meaning Many) and ‘nomial’ (in this case meaning Term)-so it means many terms.
- A polynomial is made up of terms that are only added, subtracted or multiplied.
- A quadratic polynomial in x with real coefficients is of the form ax² + bx + c, where a, b, c are real numbers with a ≠ 0.
- Degree – The highest exponent of the variable in the polynomial is called the degree of polynomial. Example: 3x3 + 4, here degree = 3.
- Polynomials of degrees 1, 2 and 3 are called linear, quadratic and cubic polynomial respectively.
- A polynomial can have terms which have Constants like 3, -20, etc., Variables like x and y and Exponents like 2 in y².
- These can be combined using addition, subtraction and multiplication but NOT DIVISION.
- The zeroes of a polynomial p(x) are precisely the x-coordinates of the points, where the graph of y = p(x) intersects the x-axis.
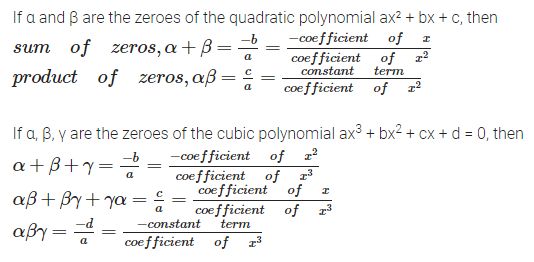
Zeroes (α, β, γ) follow the rules of algebraic identities, i.e.,
(α + β)² = α² + β² + 2αβ
∴(α² + β²) = (α + β)² – 2αβ
DIVISION ALGORITHM:
If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then
p(x) = g(x) × q(x) + r(x)
Dividend = Divisor x Quotient + Remainder
Remember this!
- If r (x) = 0, then g (x) is a factor of p (x).
- If r (x) ≠ 0, then we can subtract r (x) from p (x) and then the new polynomial formed is a factor of g(x) and q(x).
1.Zeros of Polynomial
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
2.1 INTRODUCTION :
In earlier classes, we have learnt about polynomials in one variable, their degrees, factors, multiples and zeros (or roots). In this chapter, we will study about the geometrical representation of linear quadratic and cubic polynomials and geometrical meaning of their zeros. We will also study about the relationship between the zeros and coefficients of a polynomial. LCM and HCF of two or more polynomials, rational expressions, basic operation on polynomials and concept of square root of polynomials.



2.Zeros and Coefficients of Polynomial – 1
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
Basics Revisited
Equation
An equation is a statement that two mathematical expressions having one or more variables are equal.
Linear Equation
Equations in which the powers of all the variables involved are one are called linear equations. The degree of a linear equation is always one.
General form of a Linear Equation in Two Variables
The general form of a linear equation in two variables is ax + by + c = 0, where a and b cannot be zero simultaneously.
Representing linear equations for a word problem
To represent a word problem as a linear equation
- Identify unknown quantities and denote them by variables.
- Represent the relationships between quantities in a mathematical form, replacing the unknowns with variables.
Solution of a Linear Equation in 2 variables
The solution of a linear equation in two variables is a pair of values, one for x and the other for y, which makes the two sides of the equation equal.
Eg: If 2x+y=4, then (0,4) is one of its solutions as it satisfies the equation. A linear equation in two variables has infinitely many solutions.
Geometrical Representation of a Linear Equation
Geometrically, a linear equation in two variables can be represented as a straight line.
2x – y + 1 = 0
⇒ y = 2x + 1

Graph of y = 2
x
+1
Plotting a Straight Line
The graph of a linear equation in two variables is a straight line. We plot the straight line as follows:

Any additional points plotted in this manner will lie on the same line.
All about Lines
General form of a pair of linear equations in 2 variables
A pair of linear equations in two variables can be represented as follows

The coefficients of x and y cannot be zero simultaneously for an equation.
Nature of 2 straight lines in a plane
For a pair of straight lines on a plane, there are three possibilities
i) They intersect at exactly one point

pair of linear equations which intersect at a single point.
ii) They are parallel

pair of linear equations which are parallel.
iii) They are coincident

pair of linear equations which are coincident.
Graphical Solution
Representing pair of LE in 2 variables graphically
Graphically, a pair of linear equations in two variables can be represented by a pair of straight lines.
Graphical method of finding solution of a pair of Linear Equations
Graphical Method of finding the solution to a pair of linear equations is as follows:
- Plot both the equations (two straight lines)
- Find the point of intersection of the lines.
The point of intersection is the solution.
Comparing the ratios of coefficients of a Linear Equation

Algebraic Solution
Finding solution for consistent pair of Linear Equations
The solution of a pair of linear equations is of the form (x,y) which satisfies both the equations simultaneously. Solution for a consistent pair of linear equations can be found out using
i) Elimination method
ii) Substitution Method
iii) Cross-multiplication method
iv) Graphical method
Substitution Method of finding solution of a pair of Linear Equations
Substitution method:
y – 2x = 1
x + 2y = 12
(i) express one variable in terms of the other using one of the equations. In this case, y = 2x + 1.
(ii) substitute for this variable (y) in the second equation to get a linear equation in one variable, x. x + 2 × (2x + 1) = 12
⇒ 5 x + 2 = 12
(iii) Solve the linear equation in one variable to find the value of that variable.
5 x + 2 = 12
⇒ x = 2
(iv) Substitute this value in one of the equations to get the value of the other variable.
y = 2 × 2 + 1
⇒y = 5
So, (2,5) is the required solution of the pair of linear equations y – 2x = 1 and x + 2y = 12.
Elimination method of finding solution of a pair of Linear Equations
Elimination method
Consider x + 2y = 8 and 2x – 3y = 2
Step 1: Make the coefficients of any variable the same by multiplying the equations with constants. Multiplying the first equation by 2, we get,
2x + 4y = 16
Step 2: Add or subtract the equations to eliminate one variable, giving a single variable equation.
Subtract second equation from the previous equation
2x + 4y = 16
2x – 3y = 2
– + –
———————–
0(x) + 7y =14
Step 3: Solve for one variable and substitute this in any equation to get the other variable.
y = 2,
x = 8 – 2 y
⇒ x = 8 – 4
⇒ x = 4
(4, 2) is the solution.
2.Zeros and Coefficients of Polynomial – 1
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics


Method for finding HCF of the given polynomials :
Step 1 : Express each polynomial as a product of powers of irreducible factors which also requires the numerical factors to be expressed as the product of the powers of primes.
Step 2 : If there is no common factor then HCF is 1 and if there are common irreducible factors, we find the least exponent of these irreducible factors in the factorized form of the given polynomials.
Step 3 : Raise the common irreducible factors to the smallest or the least exponents found in step 2 and take their product to get the HCF.
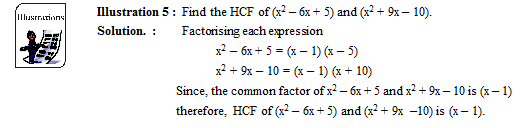
3.Zeros and Coefficients of Polynomial – 2
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
- “Polynomial” comes from the word ‘Poly’ (Meaning Many) and ‘nomial’ (in this case meaning Term)-so it means many terms.
- A polynomial is made up of terms that are only added, subtracted or multiplied.
- A quadratic polynomial in x with real coefficients is of the form ax² + bx + c, where a, b, c are real numbers with a ≠ 0.
- Degree – The highest exponent of the variable in the polynomial is called the degree of polynomial. Example: 3x3 + 4, here degree = 3.
- Polynomials of degrees 1, 2 and 3 are called linear, quadratic and cubic polynomial respectively.
- A polynomial can have terms which have Constants like 3, -20, etc., Variables like x and y and Exponents like 2 in y².
- These can be combined using addition, subtraction and multiplication but NOT DIVISION.
- The zeroes of a polynomial p(x) are precisely the x-coordinates of the points, where the graph of y = p(x) intersects the x-axis.

 Carrier Point
Carrier Point
