3.Determination of Types of Roots

Conditions Under which a Quadratic Equation has Real or Imaginary Roots

A right angled ΔABC is given in the following figure.

In this triangle, the base BC is 5 cm less than twice its height AB. The hypotenuse of the triangle is 2 cm.

Is the above given situation possible for triangle ΔABC?

Can we also find the nature of roots of a quadratic equation without solving the equation?

We can see from the above example that the value of x depends on the value under the sign of square root. If this value is positive, then the value of x will be real and if it is negative, the value of x will be imaginary.

Thus, we can say that the nature of the values of x in quadratic equation ax² + bx + c = 0, depends on the value of b² − 4ac.

Here, b² − 4ac is called the discriminant of the quadratic equation ax² + bx + c = 0. The value of b² − 4ac determines the nature of the roots of a quadratic equation.

For example: The quadratic equation 3x² − x + 2 = 0 has no real root because for this equation,

b² − 4ac = (−1)² − 4 × 3 × 2

= 1 − 24

= − 23 < 0

Here b² − 4ac < 0.

Thus, the equation 3x² − x + 2 = 0 has no real roots.

Now, let us solve some more examples based on the natures of roots of quadratic equations.

Example 1: Find the value of discriminant for the quadratic equation x² + 4x − 21 = 0.

Solution:

The given quadratic equation is x² + 4x − 21 = 0.

On comparing this equation with the standard form of quadratic equation, ax² + bx + c = 0,

we have

a = 1, b = 4, c = − 21

Therefore, the discriminant, b² − 4ac = (4)² − 4 × 1 × (− 21)

= 16 + 84

= 100

Thus, the value of discriminant for the given quadratic equation is 100.

Example 2: Find the nature of the roots of quadratic equation, x² − 8x + 16 = 0.

Solution:

The given equation is x² − 8x + 16 = 0.

On comparing this equation with the standard form of quadratic equation, ax² + bx + c = 0, we have a = 1, b = − 8, c = 16.

Therefore, the discriminant,

b² − 4ac = (− 8)² − 4 × 1 × 16

⇒ b² − 4ac = 64 − 64

⇒ b² − 4ac = 0

Thus, the given quadratic equation has two equal real roots.

Example 3: Find the value of k for which the quadratic equation x² − 12x + k = 0 has two real equal roots.

Solution:

On comparing the given equation with ax² + bx + c = 0, we have a = 1, b = − 12, c = k

For two real equal roots,

b² − 4ac = 0

⇒ (− 12)² − 4 × 1 × k = 0

⇒ 144 − 4k = 0

⇒ 4k = 144

⇒ k = 36

Thus, the value of k is 36.

Example 4: Is it possible to design a rectangular garden whose area is 250 square m and the sum of whose length and breadth is 20 m?

Solution:

Let the length of the garden be x m.

∴ Breadth = (20 − x) m

Area of garden = length × breadth

250 = x × (20 − x)

⇒ 250 = 20x − x²

⇒ x² − 20x + 250 = 0

This is a quadratic equation whose discriminant is b² − 4ac = (− 20)² − 4 × 1 × 250

= 400 − 1000

= − 600 < 0

Therefore, the roots of the equation are not real. Hence, it is not possible to design such a garden.

Example 5: Can we find two consecutive positive numbers whose product is 420? If yes, then find the numbers.

Solution:

Let one number be x.

Then the other number = x + 1

According to the question,

x × (x + 1) = 420

⇒ x² + x = 420

⇒ x² + x − 420 = 0

The discriminant of this equation is b² − 4ac = (1)² − 4 × 1 × (− 420)

= 1 + 1680

= 1681

∴ b² − 4ac > 0

Therefore, the roots of the quadratic equation x² + x − 420 = 0 are real. We can find the numbers using quadratic formula as follows

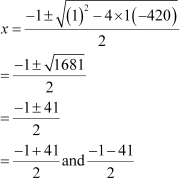
x = 20 and − 21

We take x = 20, as − 21 is a negative number.

Thus, 20 and 21 are the two consecutive positive numbers whose product is 420.