1.Tangent to a Circle

Concept Of Tangent At Any Point Of The Circle

A circle has important elements such as chords, secants, and tangents.

A tangent at any point of a circle is perpendicular to the radius through the point of contact.

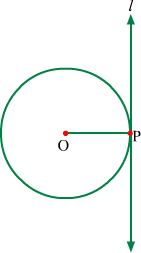
In the above figure O is the centre of circle, line l is the tangent and P is point of contact.

∴ l ∴ OP

Proof:

It is given that O is the centre of the circle, l is the tangent to this circle and P is the point of contact.

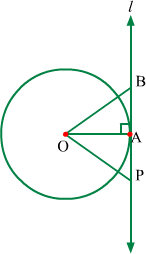
Let us assume l is not perpendicular to the radius of the circle.

In this case, let us draw perpendicular OA to tangent l. Thus, point A is distinct from point P.

Let B be any point on tangent such that BAP is a line and BA = AP.

Now, in ΔOAB and ΔOAP, we have

OA = OA (Common side)

∠OAB = ∠OAP (OA ⊥ tangent l)

BA = AP (By construction)

∴ ΔOAB ΔOAP

∴ OB = OP (By CPCT)

Since OB = OP, point B also lies on the circle.

Also, point B is different from point P.

Thus, tangent l touches the circle at two distinct points. This contradicts the definition of tangent.

Hence, our assumption is wrong.

Therefore, tangent l ⊥OP.

Hence proved.

The converse of this theorem is also true which states that:

The line perpendicular to the radius of a circle at its outer end is tangent to the circle.

Proof:

Let O be the centre of the circle, OP be the radius and l be the line perpendicular to OP such as it passes through point P on the circle.

Also, let A be any point on line l distinct from P.

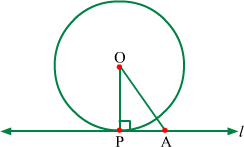
From the figure, it can be observed that ΔOAP is a right angled triangle.

∴ OA is hypotenuse for ΔOAP.

∴ OA > OP (Radius)

∴ OA is not radius.

∴ Point A does not lie on the circle.

∴ No point of line l other than P lies on the circle.

∴ P is the only point common to the circle and line l.

∴ Line l is tangent to the circle at point P. Hence proved.

Let us now solve some examples related to the tangents of the circle.

Example 1: Draw a circle with centre O, and two lines such that one is a tangent and other is a secant.

Solution:

The figure can be drawn as follows.

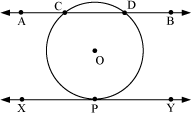
Here, 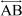is the secant, which intersects the circle at C and D and 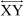is a tangent whose point of contact with the circle is P.

Example 2: Which of the following statements are correct?

(i)  There can be only one tangent at a point on the circle.

(ii)  Diameter is also a secant of the circle.

Solution:

(i)    Correct

(ii)    Incorrect

Example 3: A line XY is a tangent of the circle with centre O and radius 6 cm. The point of contact is P, and Q is any point on the tangent XY. If OQ = 10 cm, then what is the length of PQ?

Solution:

The figure can be drawn as follows.

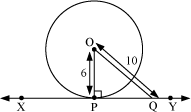
We know that the radius through the point of contact is perpendicular to the tangent.

∴ OP⊥XY

Using Pythagoras theorem in right-angled triangle OPQ, we obtain (OQ)² = (OP)² + (PQ)²

(PQ)² = (OQ⁾² – (OP)²

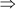(PQ)² = (10)² – (6)²

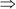(PQ)² = 100 – 36

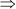(PQ)² = 64

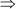PQ = 8 cm

Thus, the length of PQ is 8 cm.

Example 4: Two tangents XY and PQ are drawn at the ends of a diameter AB of the circle

with centre O. Show that XY PQ.

Solution:

The figure can be drawn as follows.

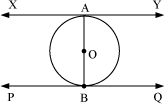
XY is a tangent at A and OA is the radius.

We know that the radius through the point of contact is perpendicular to the tangent.

∴ XY⊥OA

⇒ XY⊥AB … (1)

Similarly, PQ⊥AB … (2)

Now, the lines perpendicular to the same line are parallel.

∴ From equations (1) and (2), we obtain

XY || PQ

Hence, proved

Example 5: A circle is inscribed in a triangle such as it touches all the three sides of the triangle. Prove that the area of the triangle is half the product of its perimeter and the radius of circle.

Solution:

Let O be the centre of the circle inscribed in ΔABC.

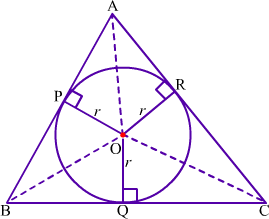
It can be seen that AB, BC and CA are tangents which touches the circle at P, Q and R respectively.

Also, OP, OQ and OR are the radii of the circle.

We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.

Therefore, AB ⊥ OP, BC ⊥ OQ and CA ⊥ OR.

Let s be the perimeter of ΔABC.

∴ s = AB + BC + CA

Now,

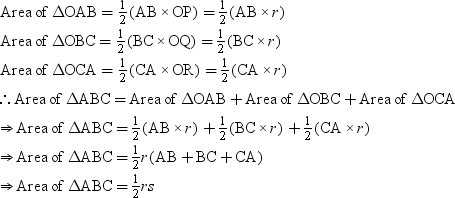
Hence proved.

Example 6: Observe the given figure.

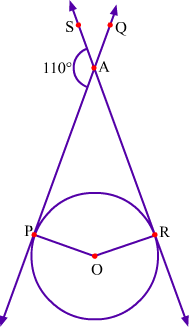
Find the angle between radii.

Solution:

In the given figure, O is the centre of the circle and OP and OR are the radii. Also, QP and SR are the tangents to the circle at points P and R respectively which intersect each other at point A.

It is given that,

∠PAS = 110°

We need to find the angle between radii OP and OR i.e., ∠POR.

From the figure, we have

∠PAS + ∠PAR = 180°

⇒ 110° + ∠PAR = 180°

⇒ ∠PAR = 180° – 110°

⇒ ∠PAR = 70°

We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.

Therefore, QP ⊥ OP and SR ⊥ OR.

∴ ∠APO = 90° and ∠ARO = 90°

Now, in quadrilateral APOR, we have

∠POR +∠APO + ∠ARO + ∠PAR = 360° (By angle sum property of quadrilaterals)

⇒ ∠POR + 90° + 90° + 70° = 360°

⇒ ∠POR + 250° = 360°

⇒ ∠POR = 110°

Thus, the angle between the radii is 110°.